题目内容
【题目】如图,△ABC中,D在AC边上,BD=CD,E在BC边上,AE=AB,过点E作EF⊥BC,交AC于F.若AD=5,CE=8,则EF的长为 . 
【答案】6
【解析】解:在AC上截取AG=BD,连接EG,作GM⊥BC于M. ∵AE=AB,BD=CD,
∴∠C=∠DBC,∠ABE=∠ABE
又∵∠AEB=∠C+∠EAC,∠ABE=∠CBD+∠DBA
∴∠ABD=∠EAC,
在△ABD和△EAG中,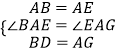 ,
,
∴△ABD≌△EAG
所以AD=EG=5,
∵AG=BD=DC,
∴AD=CG=GE=5,
∵GM⊥EC,
∴EM=CM=4,
在Rt△CMG中,GM= ![]() =3,
=3,
∵EF⊥BC,GM⊥BC,
∴MG∥EF,∵EM=MC,
∴FG=GC,
∴GM= ![]() EF,
EF,
∴EF=6.
所以答案是6.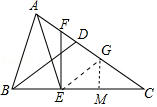
【考点精析】掌握勾股定理的概念是解答本题的根本,需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目
【题目】某生物科技发展公司投资2000万元,研制出一种绿色保健食品.已知该产品的成本为40元/件,试销时,售价不低于成本价,又不高于180元/件.经市场调查知,年销售量y(万件)与销售单价x(元/件)的关系满足下表所示的规律.
销售单价x(元/件) | … | 60 | 65 | 70 | 80 | 85 | … |
年销售量y(万件) | … | 140 | 135 | 130 | 120 | 115 | … |
(1)y与x之间的函数关系式及自变量x的取值范围。
(2)经测算:年销售量不低于90万件时,每件产品成本降低2元,设销售该产品年获利润为W(万元)(W=年销售额﹣成本﹣投资),求出年销售量低于90万件和不低于90万件时,W与x之间的函数关系式;
(3)在(2)的条件下,当销售单位定为多少时,公司销售这种产品年获利润最大?最大利润为多少万元?