Question

【题目】如图，将OA=6，AB=4的矩形OABC放置在平面直角坐标系中，动点M、N以每秒1个单位的速度分别从点A、C同时出发，其中点M沿AO向终点O运动，点N沿CB向终点B运动，当两个动点运动了t秒时，过点N作NP⊥BC，交OB于点P，连接MP．

（1）点B的坐标为；用含t的式子表示点P的坐标为；
（2）记△OMP的面积为S，求S与t的函数关系式（0＜t＜6），并求当t为何值时，S有最大值？
（3）试探究：在上述运动过程中，是否存在点T，使直线MT把△ONC分割成三角形和四边形两部分，且三角形的面积是△ONC的 ？若存在，求出点T的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）（6，4）；（t， t）
（2）

解：∵S△OMP= ×OM× t，

∴S= ×（6﹣t）× t=﹣ t2+2t=﹣ （t﹣3）2+3（0＜t＜6）．

∴当t=3时，S有最大值．

（3）

解：存在．理由如下：

由（2）得，当S有最大值时，点M、N的坐标分别为：M（3，0），N（3，4），

则直线ON的函数关系式为：y= x．

设点T的坐标为（0，b），则直线MT的函数关系式为：y=﹣ x+b，

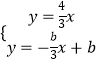解方程组 得 ，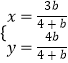

∴直线ON与MT的交点R的坐标为（ ， ），

∵S△OCN= ×4×3=6，

∴S△ORT= S△OCN=2，

①当点T在点O、C之间时，分割出的三角形是△OR1T1，

如图2所示，作R1D1⊥y轴，D1为垂足，则S△OR1T1= RD1OT= b=2．

∴3b2﹣4b﹣16=0，

解得：b= （负值舍去）．

∴b= ，

此时点T1的坐标为（0， ）．

②当点T在OC的延长线上时，分割出的三角形是△R2NE，如图，设MT交CN于点E，

由①得点E的横坐标为 ，作R2D2⊥CN交CN于点D2，则

S△R2NE= ENR2D2= （3﹣ ）（4﹣ = =2．

∴b2+4b﹣48=0，

解得：b=±2 ﹣2（负值舍去）．

∴b=2 ﹣2．

∴此时点T2的坐标为（0，2 ）．

综上所述，在y轴上存在点T1（0， ），T2（0，2 ﹣2）符合条件．

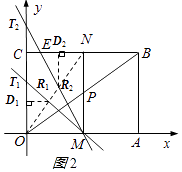
【解析】解：（1）延长NP交OA于H，如图1所示：
∵矩形OABC，
∴BC∥OA，∠OCB=90°，
∵PN⊥BC，
∴NH∥OC，
∴四边形CNHO是平行四边形，
∴OH=CN，
∵OA=6，AB=4，
∴点B的坐标为（6，4）；
由图可得，点P的横坐标=0H=CN=t，纵坐标=4﹣NP，
∵NP⊥BC，
∴NP∥OC，
∴NP：OC=BN：CB，
即NP：4=（6﹣t）：6，
∴NP=4﹣ t，
∴点P的纵坐标=4﹣NP= t，
则点P的坐标为（t， t）；
所以答案是：（6，4）；（t， t）；
【考点精析】根据题目的已知条件，利用二次函数的最值和平行四边形的判定与性质的相关知识可以得到问题的答案，需要掌握如果自变量的取值范围是全体实数，那么函数在顶点处取得最大值（或最小值），即当x=-b/2a时，y最值=(4ac-b2)/4a；若一直线过平行四边形两对角线的交点，则这条直线被一组对边截下的线段以对角线的交点为中点，并且这两条直线二等分此平行四边形的面积．