题目内容
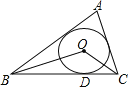
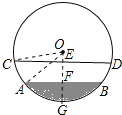
【题目】在半径为17dm的圆柱形油罐内装进一些油后,横截面如图.
(1)若油面宽AB=16dm,求油的最大深度.
(2)在(1)的条件下,若油面宽变为CD=30dm,求油的最大深度上升了多少dm?
【答案】(1)GF= 2dm;(2)油的最大深度上升了7dm.
【解析】
(1)作OF⊥AB交AB于F,交圆于G,连接OA,根据垂径定理求出AF的长,根据勾股定理求出OF,计算即可;
(2)连接OC,根据垂径定理求出CE的长,根据勾股定理求出答案.
(1)作OF⊥AB交AB于F,交圆于G,连接OA,
∴AF=![]() AB=8,
AB=8,
由勾股定理得,OF=![]() =15,
=15,
则GF=OG-OF=2dm;
(2)连接OC,
∵OE⊥CD,
∴CE=![]() EF=15,
EF=15,
OE=![]() =8,
=8,
则EF=OG-OE-FG=7dm,
答:油的最大深度上升了7dm.

练习册系列答案
相关题目
【题目】小张承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的成活率如下表所示:
移植棵数 | 成活数 | 成活率 | 移植棵数 | 成活数 | 成活率 |
50 | 47 |
| 1500 | 1335 |
|
270 | 235 |
| 3500 | 3203 |
|
400 | 369 |
| 7000 | 6335 |
|
750 | 662 |
| 14000 | 12628 |
|
下面有四个推断:
①当移植的树数是1500时,表格记录成活数是1335,所以这种树苗成活的概率是![]() ;
;
②随着移植棵数的增加,树苗成活的频率总在![]() 附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是
附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是![]() ;
;
③若小张移植10000棵这种树苗,则可能成活9000棵;
④若小张移植20000棵这种树苗,则一定成活18000棵.
其中合理的是![]()
![]()
A. ①③B. ①④C. ②③D. ②④