题目内容
【题目】为了了解中学生的身体发育情况,对某一中学同年龄的50名女学生的身高进行了测量,结果如下(单位:厘米):

完成下面的频率分布表.
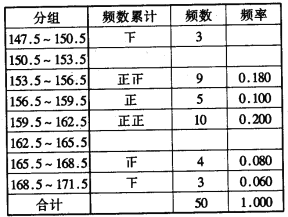
【答案】见解析.
【解析】
由每一组的频率=该组的频数:总人数得:147.5-150.5的频率=3:50=0.060;数一数150.5-153.5的频数是4,则频率=4:50=0.080;由各组频数的和等于50,则162.5-165.5之间的频数=50-3-4-9-5-10-4-3=12,则频率=12:50=0.240.
如图:
分组 | 频数累计 | 频数 | 频率 |
147.5~150.5 |
| 3 | 0.060 |
150.5~153.5 |
| 4 | 0.080 |
153.5~156.5 | 正 | 9 | 0.180 |
156.5~159.5 | 正 | 5 | 0.100 |
159.5~162.5 | 正正 | 10 | 0.200 |
162.5~165.5 | 正正 | 12 | 0.240 |
165.5~168.5 |
| 4 | 0.080 |
168.5~171.5 |
| 3 | 0.060 |
合计 | 50 | 1.000 |

 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案【题目】如图,已知y是x(x>0)的函数,表1中给出了几组x与y的对应值:
表1:
x | … |
| 1 |
| 2 |
| 3 | … |
y | … | 6 | 3 | 2 |
|
| 1 | … |
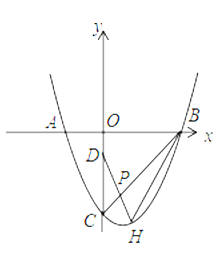
⑴以表中各对对应值为坐标,在图1的直角坐标系中描出各点,用光滑曲线顺次连接.由图像知,它是我们已经学过的哪类函数?求出函数解析式,并直接写出![]() 的值;
的值;
⑵如果一次函数图像与⑴中图像交于(1,3)和(3,1)两点,在第一、四象限内当x在什么范围时,一次函数的值小于⑴中函数的值?请直接写出答案.

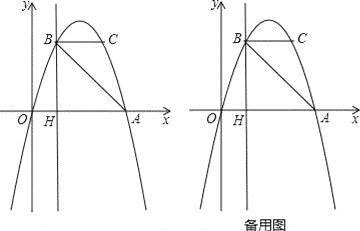
【题目】如图,在平面直角坐标系中,抛物线与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
(1)求抛物线的解析式;
(2)已知点![]() ,点
,点![]() 为线段
为线段![]() 上一动点,延长
上一动点,延长![]() 交抛物线于点
交抛物线于点![]() ,连结
,连结![]() .
.
①当四边形![]() 面积为9,求点
面积为9,求点![]() 的坐标;
的坐标;
②设![]() ,求
,求![]() 的最大值.
的最大值.
【题目】小张承包了一片荒山,他想把这片荒山改造成一个苹果园,现在有一种苹果树苗,它的成活率如下表所示:
移植棵数 | 成活数 | 成活率 | 移植棵数 | 成活数 | 成活率 |
50 | 47 |
| 1500 | 1335 |
|
270 | 235 |
| 3500 | 3203 |
|
400 | 369 |
| 7000 | 6335 |
|
750 | 662 |
| 14000 | 12628 |
|
下面有四个推断:
①当移植的树数是1500时,表格记录成活数是1335,所以这种树苗成活的概率是![]() ;
;
②随着移植棵数的增加,树苗成活的频率总在![]() 附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是
附近摆动,显示出一定的稳定性,可以估计树苗成活的概率是![]() ;
;
③若小张移植10000棵这种树苗,则可能成活9000棵;
④若小张移植20000棵这种树苗,则一定成活18000棵.
其中合理的是![]()
![]()
A. ①③B. ①④C. ②③D. ②④