题目内容
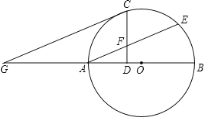
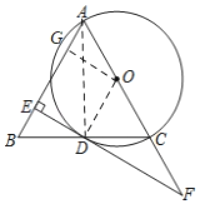
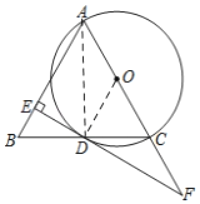
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径的⊙O与BC交于点D,DE⊥AB,垂足为E,ED的延长线与AC的延长线交于点F.
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,∠F=30°,求DE的长.

【答案】(1)详见解析;(2)DE=2![]() .
.
【解析】
(1)连接OD,AD,根据D、O是BC、AC的中点,可得OD是△ABC的中位线,OD∥AB,∠ODE=90°.
(2)先证明四边形OGED是矩形,由∠AOG=∠F=30°,得DE=OG=2![]() .
.
解:(1)连接OD,AD,
∵AC是⊙O直径,
∴AD⊥BC,
∵AB=AC,
∴点D是BC的中点,
∵O是AC的中点,
∴OD是△ABC的中位线,
∴OD∥AB,
∵DE⊥AB,
∴∠ODE=∠BED=90°,
∵OD是⊙O的半径,
∴DE是⊙O的切线;
(2)过点O作OG⊥AB于点G,
∴∠AEF=∠AGO=90°,
∴OG∥EF,四边形OGED是矩形,
∴∠AOG=∠F=30°,
∵OA=4,
∴AG=2,
由勾股定理可知:OG=2![]() ,
,
∴DE=OG=2![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目