题目内容
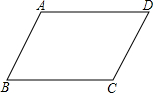如图，已知平行四边形ABCD中，∠B=60°，AB=6，BC=8．（1）建立以B为坐标原点、BC为x轴的平面直角坐标系；
（2）求A、C、D三点的坐标．
分析：（1）根据题意建立直角坐标系；
（2）过A作AE⊥BC于E，然后求出BE、AE的长，写出点A的坐标，再根据BC的长度写出点C的坐标，求出点D的横坐标，然后写出点D的坐标．
（2）过A作AE⊥BC于E，然后求出BE、AE的长，写出点A的坐标，再根据BC的长度写出点C的坐标，求出点D的横坐标，然后写出点D的坐标．
解答：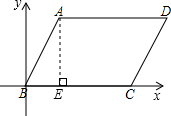
解：（1）如右图建立直角坐标系；
（2）过A作AE⊥BC于E，
∵∠B=60°，AB=6，
∴∠BAE=30°，BE=
AB=3，AE=
=
=3
，
∴A点坐标为（3，3
），
∵BC=8，
∴C点坐标为（8，0），
∵AD∥BC，且AD=BC=8，
∴D点坐标为（11，3
）．
解：（1）如右图建立直角坐标系；（2）过A作AE⊥BC于E，
∵∠B=60°，AB=6，
∴∠BAE=30°，BE=
| 1 |
| 2 |
| AB2-BE2 |
| 62-32 |
| 3 |
∴A点坐标为（3，3
| 3 |
∵BC=8，
∴C点坐标为（8，0），
∵AD∥BC，且AD=BC=8，
∴D点坐标为（11，3
| 3 |
点评：本题考查了坐标与图形性质，几何中线段的长度必是正值，而转化为点的坐标时必须注意所在象限的符号．
练习册系列答案
相关题目
CD的边长a等于点P，Q间的距离．
如图，已知平行四边形ABCD的对角线AC，BD相交于点O，BD绕点O顺时针旋转交AB，DC于E，F．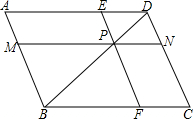
交AB、CD、AD、BC于M、N、E、F，设a=PM•PE，b=PN•PF．
23、如图，已知平行四边形ABCD．
如图，已知平行四边形ABCD，作DE⊥AB，垂足为E，把三角形AED沿AB方向平移AB长个单位长度．