Question

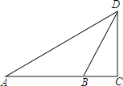
【题目】如图，在△ADC中，∠C=90°，∠A=30°．点B是线段AC上一点，且AB=40cm，∠DBC=75°．

（1）求点B到AD的距离；

（2）求线段CD的长（结果用根号表示）．

Answer 1

【答案】（1）点B到AD的距离为20cm；（2）线段CD的长为10+10．

【解析】

（1）作BE⊥AD于E，如图，在Rt△ABE中，利用30度角的性质易得BE=AB=20cm，

（2）在Rt△ABE中，利用勾股定理求出AE的长，计算出∠ADB=45°，则△BED为等腰直角三角形，所以BE=DE=20，然后利用面积法求解即可．

（1）作BE⊥AD于E，如图，

在Rt△ABE中，∵∠A=30°，

∴BE=AB=×40cm=20cm，

即点B到AD的距离为20cm；

（2）在Rt△ABE中，

AE=.

∵∠DBC=∠A+∠ADB，

∴∠ADB=75°-30°=45°，

∴△BED为等腰直角三角形，

∴BE=DE=20，

∵AD·BE =AB·CD,

∴,

∴CD=10+10．

故答案为：10+10．