جâؤ؟ؤعبف
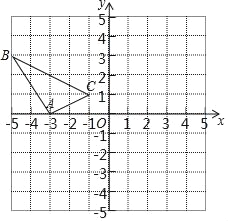
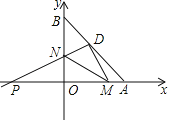
،¾جâؤ؟،؟شعئ½أوض±½ا×ّ±êدµضذ£¬µمA؛حµمB·ض±ًشعxضلµؤص°ëضل؛حyضلµؤص°ëضلةد£¬ازOA=6£¬OB=8£¬µمDتاABµؤضذµم£®
£¨1£©ض±½سذ´³ِµمDµؤ×ّ±ê¼°ABµؤ³¤£»
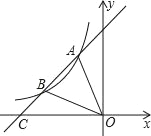
£¨2£©بôض±½ا،دNDMبئµمDذ×ھ£¬ةندكDP·ض±ً½»xضل،¢yضلسعµمP،¢N£¬ةندكDM½»xضلسعµمM£¬ء¬½سMN£®
¢ظµ±µمP؛حµمN·ض±ًشعxضلµؤ¸؛°ëضل؛حyضلµؤص°ëضلت±£¬بô،÷PDM،×،÷MON£¬اَµمNµؤ×ّ±ê£»
¢عشعض±½ا،دNDMبئµمDذ×ھµؤ¹³جضذ£¬،دDMNµؤ´َذ،تا·ٌ»ل·¢ةْ±ن»¯£؟اëثµأ÷ہيسة£®
،¾´ً°¸،؟ £¨1£©µمDµؤ×ّ±êخھ£¨3£¬4£©£¬AB=10£»£¨2£©¢ظµمNµؤ×ّ±êخھ£¨0£¬![]() £©£»¢عشعض±½ا،دNDMبئµمDذ×ھµؤ¹³جضذ£¬،دDMNµؤ´َذ،²»»ل·¢ةْ±ن»¯£¬ہيسة¼û½âخِ
£©£»¢عشعض±½ا،دNDMبئµمDذ×ھµؤ¹³جضذ£¬،دDMNµؤ´َذ،²»»ل·¢ةْ±ن»¯£¬ہيسة¼û½âخِ
،¾½âخِ،؟
£¨1£©¸ù¾فOA£½6£¬OB£½8£¬µمDتاABµؤضذµم£¬؟ةµأµمDµؤ×ّ±êخھ£¨3£¬4£©£¬¸ù¾ف¹´¹ة¶¨ہي؟ةµأAB![]() 10£»
10£»
£¨2£©¢ظدب¹µمD×÷DC،حyضلسعC£¬×÷DE،حxضلسعE£¬شٍµأ³ِCD£½3£½OE£¬DE£½4£½CO£¬،دDCN£½،دDEM£½90،م£¬شظةèON£½x£¬شٍCN£½4©پx£¬إذ¶¨،÷CDN،×،÷EDM£¬µأ³ِEM![]() £¨4©پx£©£¬إذ¶¨،÷CDN،×،÷OPN£¬µأ³ِOP
£¨4©پx£©£¬إذ¶¨،÷CDN،×،÷OPN£¬µأ³ِOP![]() £¬شظ¸ù¾فPO£½MO£¬µأ³ِ¹طسعxµؤ·½³ج
£¬شظ¸ù¾فPO£½MO£¬µأ³ِ¹طسعxµؤ·½³ج![]() £¨4©پx£©£¬اَµأxµؤضµ¼´؟ةµأµ½µمNµؤ×ّ±ê£»
£¨4©پx£©£¬اَµأxµؤضµ¼´؟ةµأµ½µمNµؤ×ّ±ê£»
¢عدب¸ù¾ف،÷CDN،×،÷EDM£¬µأµ½![]() £¬شظ¸ù¾فOA£½6£¬OB£½8£¬µأµ½
£¬شظ¸ù¾فOA£½6£¬OB£½8£¬µأµ½![]() £¬×î؛َ¸ù¾ف
£¬×î؛َ¸ù¾ف![]() £¬،دAOB£½،دNDM£½90،م£¬إذ¶¨،÷AOB،×،÷NDM£¬¸ù¾فدàثئب½اذخµؤ¶شس¦½ادàµب£¬؟ةµأ،دDMN£½،دOBA£¬½ّ¶ّµأµ½،دDMNµؤ´َذ،²»»ل·¢ةْ±ن»¯£®
£¬،دAOB£½،دNDM£½90،م£¬إذ¶¨،÷AOB،×،÷NDM£¬¸ù¾فدàثئب½اذخµؤ¶شس¦½ادàµب£¬؟ةµأ،دDMN£½،دOBA£¬½ّ¶ّµأµ½،دDMNµؤ´َذ،²»»ل·¢ةْ±ن»¯£®
£¨1£©،كOA£½6£¬OB£½8£¬µمDتاABµؤضذµم£¬،àµمDµؤ×ّ±êخھ£¨3£¬4£©£¬AB![]() 10£»
10£»
£¨2£©¢ظبçح¼£¬¹µمD×÷DC،حyضلسعC£¬×÷DE،حxضلسعE£¬شٍ
CD£½3£½OE£¬DE£½4£½CO£¬،دDCN£½،دDEM£½90،م£¬ةèON£½x£¬شٍCN£½4©پx£®
،ك،دCDE£½،دPDM£½90،م£¬،à،دCDN£½،دEDM£¬،à،÷CDN،×،÷EDM£¬،à![]() £¬¼´
£¬¼´![]() £¬،àEM
£¬،àEM![]() £¨4©پx£©£®
£¨4©پx£©£®
،كCD،خPO£¬،à،÷CDN،×،÷OPN£¬،à![]() £¬¼´
£¬¼´![]() £¬،àOP
£¬،àOP![]() £®
£®
،ك،÷PDM،×،÷MON£¬،à،دNPO£½،دNMO£¬،àPN£½MN£®
،كNO،حPM£¬،àPO£½MO£¬¼´![]() £¨4©پx£©£¬½âµأ£؛x1£½10£¨ةلب¥£©£¬x2
£¨4©پx£©£¬½âµأ£؛x1£½10£¨ةلب¥£©£¬x2![]() £¬،àON
£¬،àON![]() £¬،àµمNµؤ×ّ±êخھ£¨0£¬
£¬،àµمNµؤ×ّ±êخھ£¨0£¬![]() £©£»
£©£»
¢عشعض±½ا،دNDMبئµمDذ×ھµؤ¹³جضذ£¬،دDMNµؤ´َذ،²»»ل·¢ةْ±ن»¯£®ہيسةبçدآ£؛
سة¢ظ؟ةµأ£؛،÷CDN،×،÷EDM£¬،à![]() £¬¼´
£¬¼´![]() £®
£®
سض،كOA£½6£¬OB£½8£¬،à![]() £¬،à
£¬،à![]() £¬¼´
£¬¼´![]() £®
£®
سض،ك،دAOB£½،دNDM£½90،م£¬،à،÷AOB،×،÷NDM£¬،à،دDMN£½،دOBA£®
،ك،دOBA´َذ،²»±ن£¬،à،دDMNµؤ´َذ،²»»ل·¢ةْ±ن»¯£®