题目内容
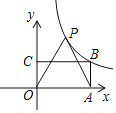
【题目】如图,已知直线y1=﹣2x经过点P(﹣2,a),点P关于y轴的对称点P′在反比例函数y2=![]() (k≠0)的图象上.
(k≠0)的图象上.
(1)求点P的坐标;
(2)求反比例函数的解析式,并直接写出当y2<2时自变量x的取值范围.
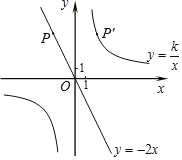
【答案】(1)P(﹣2,4);(2)y=![]() ;x<0或x>4;
;x<0或x>4;
【解析】
(1)利用待定系数法把P(-2,a)代入函数关系式y1=-2x中即可求出P点坐标;
(2)利用待定系数法把P'的坐标代入反比例函数y2=![]() (k≠0)中,即可算出k的值,进而可得到反比例函数关系式,再结合图象可以直接写出答案.
(k≠0)中,即可算出k的值,进而可得到反比例函数关系式,再结合图象可以直接写出答案.
(1)将M(﹣2,a)代入y=﹣2x中得:a=﹣2×(﹣2)=4,
∴P(﹣2,4),
(2)∵P(﹣2,4),
∴P'(2,4),
将(2,4)代入y=![]() 中得:k=8
中得:k=8
∴反比例函数的解析式为y=![]() ,
,
由图象得:当y2<2时自变量x的取值范围:x<0或x>4.

练习册系列答案
相关题目