题目内容
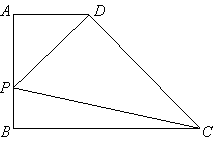
【题目】已知:如图,![]() ⊥
⊥![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上,联结
上,联结![]() ,过点
,过点![]() 作
作![]() 的垂线,与
的垂线,与![]() 相交于点
相交于点![]() .设线段
.设线段![]() 的长为
的长为![]() .
.
(1)当![]() 时,求线段
时,求线段![]() 的长;
的长;
(2)设△![]() 的面积为
的面积为![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出函数的定义域;
的函数解析式,并写出函数的定义域;
(3)当△![]() ∽△
∽△![]() 时,求线段
时,求线段![]() 的长.
的长.
【答案】(1)![]() (2)
(2)![]() ,0 < x ≤ 3(3)4或
,0 < x ≤ 3(3)4或![]()
【解析】(1)过点![]() 作
作![]() ⊥
⊥![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
∵![]() ,
,![]() ,PD⊥CD,AD // BC,
,PD⊥CD,AD // BC,
∴∠![]() =∠
=∠![]() =∠
=∠![]() = 90°,
= 90°,
![]() .
.
∵![]() //
// ![]() ,
,
∴![]() .即得
.即得![]() .
.
又∵![]() ,
,
![]() ,
,
∴![]() .
.
又由![]() ,得 △
,得 △![]() ∽△
∽△![]() .
.
∴![]() .
.
于是,由![]() ,得
,得 ![]() . (2分)
. (2分)
在![]() △
△![]() 和
和![]() △
△![]() 中,
中,
得 ![]() ,
,![]() . (1分)
. (1分)
于是,在![]() △
△![]() 中,得
中,得 ![]() . (1分)
. (1分)
(2)在Rt△![]() 中,由
中,由 ![]() ,
,![]() ,
,
得![]() . (1分)
. (1分)
∵△![]() ∽△
∽△![]() ,
,
∴![]() .
.
∴![]() . (1分)
. (1分)
在![]() △
△![]() 中,
中,![]() .
.
∴所求函数解析式为![]() . (2分)
. (2分)
函数的定义域为 0 < x ≤ 3. (1分)
(3)当△![]() ∽△
∽△![]() 时,即得△img src="http://thumb.zyjl.cn/questionBank/Upload/2019/04/06/13/515cbe93/SYS201904061302267942123906_DA/SYS201904061302267942123906_DA.035.png" width="37" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />∽△
时,即得△img src="http://thumb.zyjl.cn/questionBank/Upload/2019/04/06/13/515cbe93/SYS201904061302267942123906_DA/SYS201904061302267942123906_DA.035.png" width="37" height="17" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />∽△![]() ∽△
∽△![]() . (1分)
. (1分)
根据题意,当△![]() ∽△
∽△![]() 时,有下列两种情况:
时,有下列两种情况:
(ⅰ)当点![]() 与点
与点![]() 不重合时,可知
不重合时,可知 ![]() .
.
由△![]() ∽∽△
∽∽△![]() ,得
,得![]() .即得
.即得![]() .
.
由△![]() ∽△
∽△![]() ,得
,得![]() .
.
∴![]() .即得
.即得![]() .
.
∴![]() .
.
易证得四边形![]() 是矩形,
是矩形,
∴![]() . (2分)
. (2分)
(ⅱ)当点![]() 与点
与点![]() 重合时,可知
重合时,可知 ![]() .
.
在Rt△![]() 中,由
中,由![]() ,
,![]() ,得
,得![]() .
.
由△![]() ∽△
∽△![]() ,得
,得![]() .
.
即得![]() .
.
解得![]() . (2分)
. (2分)
∴△![]() ∽△
∽△![]() 时,线段
时,线段![]() 的长分别为4或
的长分别为4或![]() .
.
(1)过点![]() 作
作![]() ⊥
⊥![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,证出△
,证出△![]() ∽△
∽△![]() ,从而得出DE的长,然后根据勾股定理得出PD与DC的长,再根据勾股定理得出PC的长;
,从而得出DE的长,然后根据勾股定理得出PD与DC的长,再根据勾股定理得出PC的长;
(2)先求出PD的长,然后根据△![]() ∽△
∽△![]() ,算出CD的长,再利用三角形面积公式得出它的解析式;
,算出CD的长,再利用三角形面积公式得出它的解析式;
(3)分点P与点B重合不重合两种情况进行讨论。

 阅读快车系列答案
阅读快车系列答案