Question

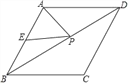
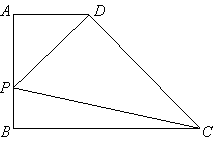
【题目】如图，在□ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE＝CG，AH＝CF．

（1）求证：△AEH≌△CGF；

（2）若EG平分∠HEF，求证：四边形EFGH是菱形．

Answer 1

【答案】（1）答案见解析；（2）答案见解析．

【解析】试题分析：（1）根据全等三角形的判定定理SAS证得结论；

（2）欲证明四边形EFGH是菱形，只需推知四边形EFGH是平行四边形，然后证得该平行四边形的邻边相等即可．

试题解析：证明：（1）∵四边形ABCD是平行四边形，∴∠A=∠C，在△AEH与△CGF中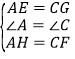，∵，∴△AEH≌△CGF（SAS）；

（2）∵四边形ABCD是平行四边形，∴AD=BC，AB=CD，∠B=∠D．

∵AE=CG，AH=CF，∴EB=DG，HD=BF，∴△BEF≌△DGH，∴EF=HG．

又∵△AEH≌△CGF，∴EH=GF，∴四边形HEFG为平行四边形，∴EH∥FG，∴∠HEG=∠FGE．∵EG平分∠HEF，∴∠HEG=∠FEG，∴∠FGE=∠FEG，∴EF=GF，∴四边形EFGH是菱形．