题目内容
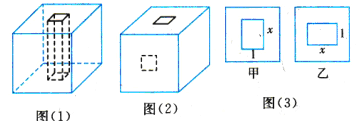
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:
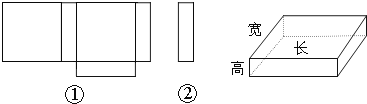
(1)小明总共剪开了 条棱.
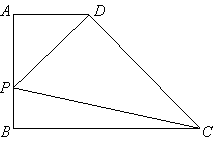
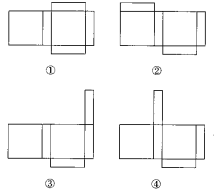
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在图上补 全.(请在备用图中画出所有可能)
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的4倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是720cm,求这个长方体纸盒的体积.
【答案】(1)8,
(2)四种可能,图形见详解
(3)128000 cm2
【解析】
(1)根据展开后的图形即可解题,(2)根据长方体的展开图的特点,进行画图,注意考虑周全.,(3)利用底面是正方形, 最长的一条棱是最短的一条棱的4倍,棱长的和是720cm,求出长宽高,即可解题.
解:(1)由展开图发现,小明一共剪开了8条棱,
故答案是8,
(2)如下图,四种可能,
(3)∵长方体纸盒的底面是一个正方形,
∴设最短的棱长即高为acm,则长与宽相等为4acm.
∵长方体纸盒所有棱长的和是720cm,∴4(a+4a+4a)=720,解得a=20
这长方体纸盒的体积为20×80×80=128000cm2
故答案是8;四种情况;128000 cm2

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目