��Ŀ����
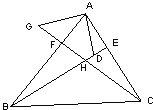
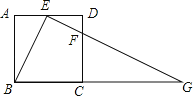
����Ŀ����֪����ABCD�У�AD=6����ACB=30��������ACD�Ƶ�C˳ʱ����ת�õ���EFG��ʹ��D�Ķ�Ӧ��G����BC�ӳ����ϣ���A��Ӧ��ΪE�㣬C���Ӧ��ΪF�㣬F����C���غϣ���ͼ1������ʱ����EFG��ÿ��1����λ���ȵ��ٶ���ֱ��CB����ƽ�ƣ�ֱ����G���B�غ�ʱֹͣ�˶�������EFG�˶���ʱ��Ϊt��t��0����
��1����tΪ��ֵʱ����D�����߶�EF�ϣ�
��2������ƽ�ƹ�������EFG�����ABCD�ص����ֵ����ΪS����ֱ��д��S��t֮��ĺ�����ϵʽ����д����Ӧ��t��ȡֵ��Χ��
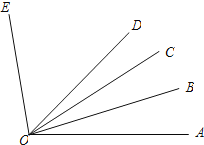
��3����ƽ�ƹ����У�����G���B�غ�ʱ����ͼ2��������CBA�Ƶ�B��ʱ����ת�õ���C1A1B��ֱ��EF��C1A1����ֱ�߽���P�㣬��C1B����ֱ�߽��ڵ�Q������ת�����У���ABC����ת��Ϊ����0�㣼����180�㣩���Ƿ���������Ħ���ʹ����C1PQΪ���������Σ������ڣ���д�����Ķ������������ڣ���˵�����ɣ�
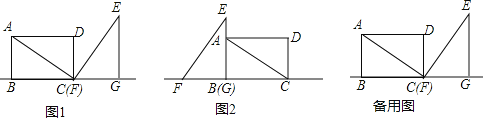
���𰸡���1����t=2ʱ����D�����߶�EF�ϣ���2������������3����C1PQΪ���������Σ���ת��Ϊ30�㡢120�㡢165�㣮
��������
�����������1���������Ǻ�������߶�CD���ӳ�AD��EF�ڵ�H���������Ǻ�����������߶�DH���ȣ��ٳ����˶��ٶȼ�Ϊ�˶�ʱ�䣻
��2������������������ۣ�����غ������д��S����t�ĺ�����ϵʽ���ɣ�
��3��ͨ��������C1PQΪ���������Σ���������������ֱ������Ӧ�Ƕȼ��ɣ�
�⣺��1����AD=BC=6����ACB=30����
��AB=DF=6��tan30��=2![]() ��
��
�ӳ�AD��EF�ڵ�H������ͼ��
�ߡ�ACD�Ƶ�C˳ʱ����ת�õ���EFG��
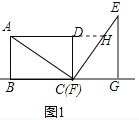
���DFH=30����
��DH=DF��tan30��=2��
�ߡ�EFG��ÿ��1����λ���ȵ��ٶ���ֱ��CB����ƽ�ƣ�2��1=2�룬
����t=2ʱ����D�����߶�EF�ϣ�
��2����0��t��2ʱ��S=![]() t2��
t2��
��2��t��2![]() ʱ��S=2
ʱ��S=2![]() t��2
t��2![]() ��
��
��2![]() ��t��6ʱ��S=12��2
��t��6ʱ��S=12��2![]() ��
��
��6��t��8ʱ��S=��![]() t2+6
t2+6![]() t��20
t��20![]() +12��
+12��
��8��t��6+2![]() ʱ��S=��2
ʱ��S=��2![]() t+12
t+12![]() +12��
+12��
��3��30�㡢120�㡢165�㣮
�ߡ�C1PQΪ���������Σ�
��PQ=PC�䣬����ͼ��
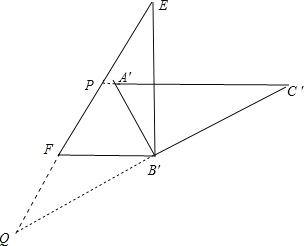
����Q=��C��=30����
���EPC��=60����
�ߡ�E=30����
���A��B��E=30����
����=30����
ͬ������PQ=QC�䣬PC��=QC�䣬��=120�㡢165�㣮
���C1PQΪ���������Σ���ת��Ϊ30�㡢120�㡢165�㣮

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д� ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д�