题目内容
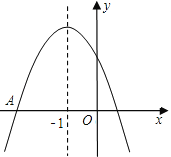
【题目】如图是二次函数y=ax2+bx+c图象的一部分，图象过点A（﹣3，0），对称轴为x=﹣1．给出四个结论：①b2＞4ac；②2a+b=0；③a﹣b+c=0；④5a＜b．其中正确的有（ ）
A．1个 B．2个 C．3个 D．4个
【答案】B
【解析】
试题分析：由抛物线的开口向下知a＜0，与y轴的交点在y轴的正半轴上得到c＞0，由对称轴为x=
=﹣1可以判定②错误，由图象与x轴有交点，对称轴为x==﹣1，与y轴的交点在y轴的正半轴上，可以推出b2﹣4ac＞0，即b2＞4ac，①正确，由x=﹣1时y有最大值，由图象可知y≠0，③错误，然后即可作出选择．
解：①∵图象与x轴有交点，对称轴为x==﹣1，与y轴的交点在y轴的正半轴上，
又∵二次函数的图象是抛物线，
∴与x轴有两个交点，
∴b2﹣4ac＞0，
即b2＞4ac，故本选项正确，
②∵抛物线的开口向下，
∴a＜0，
∵与y轴的交点在y轴的正半轴上，
∴c＞0，
∵对称轴为x==﹣1，
∴2a=b，
∴2a+b=4a，a≠0，
故本选项错误，
③∵x=﹣1时y有最大值，
由图象可知y≠0，故本选项错误，
④把x=1，x=﹣3代入解析式得a+b+c=0，9a﹣3b+c=0，
两边相加整理得5a﹣b=﹣c＜0，即5a＜b，故本选项正确．
故选B．
练习册系列答案
相关题目
【题目】张华记录了今年雨季钱塘江一周内水位变化的情况如下表（正号表示比前一天高，负号表示比前一天低）：
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化（m） | +0.25 | +0.80 | ﹣0.40 | +0.03 | +0.28 | ﹣0.36 | ﹣0.04 |
（1）本周星期 水位最高，星期 水位最低．
（2）与上周末相比，本周日的水位是上升了还是下降了？（写出计算过程）
（2）请用折线统计图表示钱塘江一周内水位变化的情况．
