题目内容
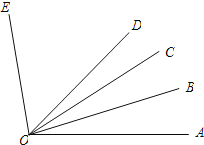
【题目】已知∠AOB=20°,∠AOE=100°,OB平分∠AOC,OD平分∠AOE.
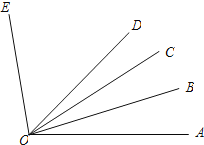
(1)求∠COD的度数;
(2)若以O为观察中心,OA为正东方向,射线OD的方向角是 ;
(3)若∠AOE的两边OA、OE分别以每秒5°、每秒3°的速度,同时绕点O逆时针方向旋转,当OA回到原处时,OA、OE停止运动,则经过几秒,∠AOE=42°.
【答案】(1)10°;(2)北偏东40°;(3)29或71秒
【解析】
试题分析:(1)根据图示得到∠EOB=80°;然后由角平分线的定义来求∠COD的度数;
(2)根据方向角的表示方法,可得答案;
(3)设经过x秒,∠AOE=42°则依据题意列出方程并解答即可.
解:(1)∵∠AOB=20°,∠AOE=100°,
∴∠EOB=∠AOE﹣∠AOB=80°.
又∵OB平分∠AOC,OD平分∠AOE,
∴∠AOC=2∠AOB=40°,∠AOD=![]() ∠AOE=50°,
∠AOE=50°,
∴∠COD=∠AOD﹣∠AOC=50°﹣40°=10°;
(2)由(1)知,∠AOD=50°,
射线OD在东偏北50°,即射线OD在北偏东40°;
故答案是:北偏东40°;
(3)设经过x秒,∠AOE=42°则
3x﹣5x+100°=42°,或5x﹣(3x+100)=42,
解得 x=29或x=71.
即经过29或71秒,∠AOE=42°.

练习册系列答案
相关题目