题目内容
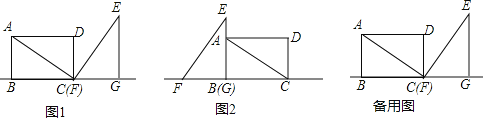
【题目】如图,在正方形ABCD中,E、F分别是边AD、CD上的点,AE=ED,DF=![]() DC,连接EF并延长交BC的延长线于点G.
DC,连接EF并延长交BC的延长线于点G.
(1)求证:△ABE∽△DEF;
(2)若正方形的边长为4,求BG的长.
【答案】(1)见解析;(2)10
【解析】
试题分析:(1)利用正方形的性质,可得∠A=∠D,根据已知可得![]() ,根据有两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;
,根据有两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF;
(2)根据平行线分线段成比例定理,可得CG的长,即可求得BG的长.
(1)证明:∵ABCD为正方形,
∴AD=AB=DC=BC,∠A=∠D=90°,
∵AE=ED,
∴![]() ,
,
∵DF=![]() DC,
DC,
∴![]() ,
,
∴![]() ,
,
∴△ABE∽△DEF;
(2)解:∵ABCD为正方形,
∴ED∥BG,
∴![]() ,
,
又∵DF=![]() DC,正方形的边长为4,
DC,正方形的边长为4,
∴ED=2,CG=6,
∴BG=BC+CG=10.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
【题目】张华记录了今年雨季钱塘江一周内水位变化的情况如下表(正号表示比前一天高,负号表示比前一天低):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化(m) | +0.25 | +0.80 | ﹣0.40 | +0.03 | +0.28 | ﹣0.36 | ﹣0.04 |
(1)本周星期 水位最高,星期 水位最低.
(2)与上周末相比,本周日的水位是上升了还是下降了?(写出计算过程)
(2)请用折线统计图表示钱塘江一周内水位变化的情况.