题目内容
如图，一个油桶靠在墙边，量得WY=2m，并且XY⊥WY，这个油桶的底面半径是______m．
连接OX、OW，如图，
∵XY⊥WY，OX⊥XY，OW⊥WY，OW=OX，
∴四边形OXYW为正方形，
∴OW=WY，
∵WY=2m，
∴这个油桶的底面半径是2m．
故答案为：2．
∵XY⊥WY，OX⊥XY，OW⊥WY，OW=OX，
∴四边形OXYW为正方形，
∴OW=WY，
∵WY=2m，
∴这个油桶的底面半径是2m．
故答案为：2．
练习册系列答案
相关题目
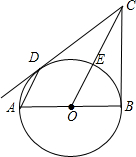
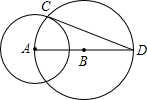
延长线分别交AC、BC于点G、F．
OE=1cm，DF=4cm．