题目内容
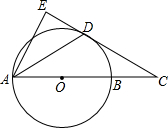
如图，已知AB是⊙O的直径，BC与⊙O相切于点B，连接OC，交⊙O于点E，弦AD∥OC．
（1）求证：点E是弧BD的中点；（2）求证：CD是⊙O的切线．
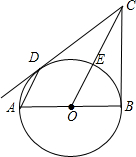
（1）求证：点E是弧BD的中点；（2）求证：CD是⊙O的切线．
证明：（1）连接OD．
∵AD∥OC，
∴∠ADO=∠COD，∠A=∠COB． （1分）
∵OA=OD，
∴∠A=∠ADO． （2分）
∴∠COD=∠COB．（3分）
∴弧BE=弧DE，即点E是弧BD的中点． （4分）
（2）由（1）可知∠COD=∠COB，
在△COD和△COB中，
，（5分）
∴△COD≌△COB，
∴∠CDO=∠CBO．（6分）
∵BC与⊙O相切于点B，
∴BC⊥OB，即∠CBO=90°． （7分）
∴∠CDO=90°，即DC⊥OD．
∴CD是⊙O的切线． （8分）
∵AD∥OC，
∴∠ADO=∠COD，∠A=∠COB． （1分）
∵OA=OD，
∴∠A=∠ADO． （2分）
∴∠COD=∠COB．（3分）
∴弧BE=弧DE，即点E是弧BD的中点． （4分）
（2）由（1）可知∠COD=∠COB，
在△COD和△COB中，
|
∴△COD≌△COB，
∴∠CDO=∠CBO．（6分）
∵BC与⊙O相切于点B，
∴BC⊥OB，即∠CBO=90°． （7分）
∴∠CDO=90°，即DC⊥OD．
∴CD是⊙O的切线． （8分）
练习册系列答案
阅读快车系列答案
相关题目
为
