题目内容
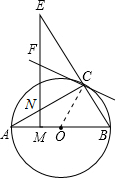
如图,AB是⊙O的直径,且点C为⊙O上的一点,∠BAC=30°,M是OA上一点,过M作AB的垂线交AC于点N,交BC的延长线于点E,直线CF交EN于点F,且∠ECF=∠E.
(1)证明:CF是⊙O的切线;
(2)设⊙O的半径为1,且AC=CE,求MO的长.

(1)证明:CF是⊙O的切线;
(2)设⊙O的半径为1,且AC=CE,求MO的长.

(1)证明:如图,连接OC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=30°,
∴∠ABC=60°;
在Rt△EMB中,∵∠E+∠MBE=90°,
∴∠E=30°;
∵∠E=∠ECF,
∴∠ECF=30°,
∴∠ECF+∠OCB=90°;
∵∠ECF+∠OCB+∠OCF=180°,
∴∠OCF=90°,
∴CF为⊙O的切线;
(2)在Rt△ACB中,∠A=30°,∠ACB=90°,
∴AC=ABcos30°=
,BC=ABsin30°=1;
∵AC=CE,
∴BE=BC+CE=1+
,在Rt△EMB中,∠E=30°,∠BME=90°,
∴MB=BEsin30°=
,
∴MO=MB-OB=
.
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=30°,
∴∠ABC=60°;
在Rt△EMB中,∵∠E+∠MBE=90°,
∴∠E=30°;
∵∠E=∠ECF,
∴∠ECF=30°,
∴∠ECF+∠OCB=90°;
∵∠ECF+∠OCB+∠OCF=180°,
∴∠OCF=90°,
∴CF为⊙O的切线;
(2)在Rt△ACB中,∠A=30°,∠ACB=90°,
∴AC=ABcos30°=
| 3 |
∵AC=CE,
∴BE=BC+CE=1+
| 3 |
∴MB=BEsin30°=
1+
| ||
| 2 |
∴MO=MB-OB=
-1+
| ||
| 2 |


练习册系列答案
相关题目