题目内容
长方形ABCD中,AB=1,AD=
,以点B为圆心,BA长为半径作圆交BC于点E.在弧AE上找一点P,使过点P的⊙B的切线平分长方形的面积.设此切线交AD于点S,交BC于点T,则ST的长为______.

| 3 |

连接BD,∵AB=1,AD=
,
∴BD=2,∠PBC=30°,
而AB=1,
∴BD与弧AE的交点为BD的中点,即为P点,过P作⊙B的切线平分长方形,如图,
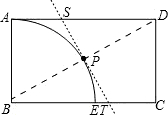
∴BD⊥ST,且PT=PS,
∵PT=BP•tan30°=
BP=
,
∴ST=
.
故答案为:
.
| 3 |
∴BD=2,∠PBC=30°,
而AB=1,
∴BD与弧AE的交点为BD的中点,即为P点,过P作⊙B的切线平分长方形,如图,

∴BD⊥ST,且PT=PS,
∵PT=BP•tan30°=
| ||
| 3 |
| ||
| 3 |
∴ST=
2
| ||
| 3 |
故答案为:
2
| ||
| 3 |

练习册系列答案
相关题目
 为
为






