题目内容
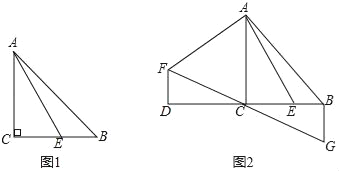
【题目】如图，小明为了测量大楼AB的高度，他从点C出发，沿着斜坡面CD走260米到点D处，测得大楼顶部点A的仰角为37°，大楼底部点B的俯角为45°，已知斜坡CD的坡度为i=1：2.4．则大楼AB的高度约为（ ）米．
（参考书据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）
A. 170 B. 175 C. 180 D. 190
【答案】B
【解析】
作DE⊥AB于E，作DF⊥BC于F，y由CD的坡度为i=1：2.4，CD=104米，得到
=1：2.4，根据勾股定理列方程，即可得到DF的长度；根据矩形的性质得到BE=DF，由等腰直角三角形的性质得到DE=BE=40m，根据三角函数的定义即可得到结果．
作DE⊥AB于E，作DF⊥BC于F，则四边形DFBE是矩形．
∵CD的坡度为i=1：2.4，CD=260，∴=1：2.4，∴
=260，∴DF=100；
∵四边形DFBE是矩形，∴BE=100．
∵∠BDE=45°，∴DE=BE=100．在Rt△ADE中，∠ADE=37°，∴AE=tan37°100=75，∴AB=AE+BE=175（米）．
故选B．
练习册系列答案
黄冈小状元同步计算天天练系列答案
相关题目
