题目内容
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k≠0)的图象与一次函数y=ax+b(a≠0)的图象交于A、B两点,过点A作AH⊥y轴,垂足为H,若OH=4,sin∠AOH=
(k≠0)的图象与一次函数y=ax+b(a≠0)的图象交于A、B两点,过点A作AH⊥y轴,垂足为H,若OH=4,sin∠AOH=![]() ,点B的坐标(6,n).
,点B的坐标(6,n).
(1)求反比例函数和一次函数的解析式.
(2)求△AOB的面积.

【答案】(1)y=![]() ,y=﹣
,y=﹣![]() x+6(2)9
x+6(2)9
【解析】
(1)通过解直角三角形可得出点A的坐标,利用反比例函数图象上点的坐标特征可求出反比例函数解析式,再根据反比例函数图象上点的坐标特征可得出点B的坐标,根据点A、B的坐标利用待定系数法,即可求出一次函数的解析式;
(2)利用一次函数图象上点的坐标特征求出点C的坐标,再根据△AOB的面积=△AOC的面积﹣△COB的面积即可求解.
(1)∵在Rt△AOH中,∠AHO=90°,OH=4,sin∠AOH=![]() ,∴AH=3,OA=5,∴点A的坐标为(3,4).
,∴AH=3,OA=5,∴点A的坐标为(3,4).
∵点A在反比例函数y=![]() (k≠0)的图象上,∴k=3×4=12,∴反比例函数的解析式为y=
(k≠0)的图象上,∴k=3×4=12,∴反比例函数的解析式为y=![]() .
.
∵点B的坐标为(6,n),点B在反比例函数y=![]() 的图象上,∴n=
的图象上,∴n=![]() =2,∴点B的坐标为(6,2).
=2,∴点B的坐标为(6,2).
将点A(3,4)、B(6,2)代入y=ax+b中,![]() ,解得:
,解得: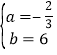 ,∴一次函数的解析式为y=﹣
,∴一次函数的解析式为y=﹣![]() x+6;
x+6;
(2)当y=0时,﹣![]() x+6=0,解得:x=9,∴点C的坐标为(9,0),∴S△AOB=S△AOC﹣S△COB
x+6=0,解得:x=9,∴点C的坐标为(9,0),∴S△AOB=S△AOC﹣S△COB
=![]() ×9×4﹣
×9×4﹣![]() ×9×2
×9×2
=18﹣9
=9.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目