题目内容
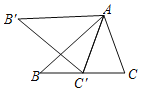
【题目】如图，在△ABC中，∠B＝42°，把△ABC绕着点A顺时针旋转，得到△AB'C'，点C的对应点C'落在BC边上，且B'A∥BC，则∠BAC'的度数为（ ）
A.24°B.25°C.26°D.27°
【答案】D
【解析】
由旋转的性质得出∠B'＝∠B＝42°，∠AC'B'＝∠C，AC'＝AC，由AC'＝AC得出∠AC'C＝∠C＝∠AC'B'，由B'A∥BC得出∠B'C'C＝138°，求出∠AC'C＝∠C＝∠AC'B='69°，再由三角形的外角性质即可得出答案．
解：由旋转的性质得：∠B'＝∠B＝42°，∠AC'B'＝∠C，AC'＝AC，
∴∠AC'C＝∠C＝∠AC'B'，
∵B'A∥BC，
∴∠B'+∠B'C'C＝180°，
∴∠B'C'C＝180°﹣42°＝138°，
∴∠AC'C＝∠C＝∠AC'B'＝
×138°＝69°，
∴∠BAC'＝∠AC'C﹣∠B＝69°﹣42°＝27°；
故选：D．
练习册系列答案
云南师大附小一线名师提优作业系列答案
冲刺100分单元优化练考卷系列答案
相关题目
