题目内容
【题目】如图,∠AOB=120°,OC平分∠AOB,∠MCN=60°,CM与射线OA相交于M点,CN与直线BO相交于N点.把∠MCN绕着点C旋转.
(1)如图1,当点N在射线OB上时,求证:OC=OM+ON;
(2)如图2,当点N在射线OB的反向延长线上时,OC与OM,ON之间的数量关系是 (直接写出结论,不必证明)

【答案】(1)证明见解析;(2)OC=OM﹣ON,理由见解析.
【解析】
(1)作∠OCG=60°,交OA于G,可得△OCG是等边三角形,得再证明△OCN≌△GCM(ASA)问题可解;
(2)仿照(1)中的解法.问题可解
(1)证明:如图

作∠OCG=60°,交OA于G,
∵∠AOB=120°,OC平分∠AOB,
∴∠CON=∠COG=60°,
∴∠OCG=∠COG,
∴OC=CG,
∴△OCG是等边三角形,
∴OC=OG,∠CGM=60°=∠CON,
∵∠MCN=∠OCG=60°,
∴∠OCN=∠GCM,
在△OCN和△GCM中,
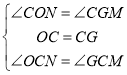 ,
,
∴△OCN≌△GCM(ASA),
∴ON=GM,
∵OG=OM+GM,
∴OC=OM+ON;
(2)解:OC=OM﹣ON,理由如下:
如图:

作∠OCG=60°,交OA于G,:
∵∠AOB=120°,OC平分∠AOB,
∴∠CON=∠COG=60°,
∴∠CON=120°,∠OCG=∠COG,
∴OC=CG,
∴△OCG是等边三角形,
∴OC=OG,∠CGO=60°,
∴∠CGM=120°=∠CON,
∵∠MCN=∠OCG=60°,
∴∠OCN=∠GCM,
在△OCN和△GCM中,
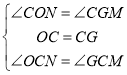 ,
,
∴△OCN≌△GCM(ASA),
∴ON=GM,
∵OG=OM﹣GM,
∴OC=OM﹣ON;
故答案为:OC=OM﹣ON

练习册系列答案
相关题目