��Ŀ����
����Ŀ������һ����һ����Ȼ���ĸ�λ���ֽ�̫�������µ������ϸ�λ����4�����������13�ı�������ԭ���ܱ�13�����������̫�������Ƿ�13�ı��������ظ���������β��������ӡ���͡��Ĺ��̣�ֱ��������ж�Ϊֹ�����磬�ж�377�Ƿ�13�ı����Ĺ������£�37+7��4��65��65��13��5�����ԣ�377��13�ı������������ж�8632�Ƿ�13�ı����Ĺ������£�863+2��4��871��87+1��4��91��91��13��7�����ԣ�8632��13�ı�����
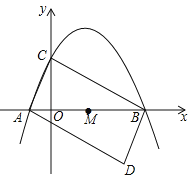
���϶�����һ����λ��Ȼ��n������ǧλ���λ��ͬ����λ��ʮλ��ͬ�����dz������Ϊ���Գ������������Գ�����n��ǰ��λ�����λ����λ�õõ�һ���µ�n������F��n����![]() ������n��3113��n����1331����3113����
������n��3113��n����1331����3113����![]() ��18��
��18��
��1�����ò���һ�ķ����ж�1326��3366�ܷ�13������
��2����m��p�����Գ�����������m��![]() ��p��
��p��![]() ��0��b��a��5��1��c��a��5��a��b��c��Ϊ����������m�ܱ�l3��������F��m����F��p����36����p��
��0��b��a��5��1��c��a��5��a��b��c��Ϊ����������m�ܱ�l3��������F��m����F��p����36����p��
���𰸡�(1)������;(2)p��2332��
��������
��1�����ò���һ�ķ��������жϼ��ɣ�
��2����m�ܱ�13�������ɵ�b=0��a=2��3��4��5�������Գ���������ɵ�9��a-b��-9��c-a��=36������p��ֵ��
�⣺��1����132+6��4��156��15+6��4��39��
��1326�ܱ�13������
��336+6��4��360��36+0��4��36��
��3366���ܱ�13������
��2����m�ܱ�13����
��100a+10b+b+4a��104a+11b�ܱ�13����
��b��0��
��0��b��a��5��1��c��a��5��
��a��2��3��4��5��
��F��m����![]() ��9��a��b����
��9��a��b����
F��p����![]() ��9��c��a����
��9��c��a����
��9��a��b����9��c��a����36��
��2a��c��4
��a��2ʱ��c��0����ȥ����
��a��3ʱ��c��2��2��3��
��p��2332��
��a��4ʱ��c��4����ȥ����
��a��5ʱ��c��6����ȥ����
����������p��2332��

����Ŀ���ݡ��������������ܣ���2009��ʹ�����Ժ��ȽӴ������״�ͻ��1000���˴�֮��ÿ��Ӵ���������������2018��ͻ��1700���˴Σ���Ϊ�����ϽӴ������IJ���ݣ��ر������š����ڹʹ���������������ˣ��ʹ�����һ�������IJ���Ŀ�IJ�����������ٴ�����ʹ��ȣ����ǹʹ��Ĵ�Ӫ����ԱΪ������Բ�ͬ����Ⱥ����Ĵ���Ʒ����������˲��ֲι۹ʹ��Ĺ��ڵ����䣬����������������ͳ��ͼ����
2018��ι۹ʹ���������Ƶ���ֲ���
����x/�� | Ƶ��/���� | Ƶ�� |
20��x��30 | 80 | b |
30��x��40 | a | 0.240 |
40��x��50 | 35 | 0.175 |
50��x��60 | 37 | c |
�ϼ� | 200 | 1.000 |
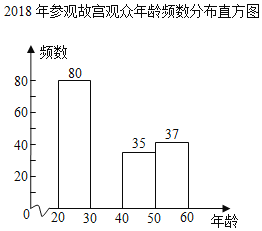
��1�������a��b��c��ֵ��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3���������Ͽ���������ڣ�20��x��40���Ѿ���Ϊ�ι۹ʹ�����ҪȺ�壮�������ι۹ʹ������ﵽ2000���˴Σ���ô�����������Ԥ��Լ�� ���˴Σ�