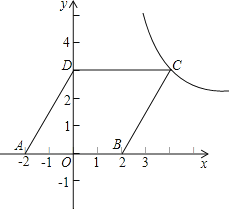题目内容
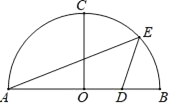
【题目】如图,AB是半圆O的直径,半径OC⊥AB,OB=4,D是OB的中点,点E是弧BC上的动点,连接AE,DE.
(1)当点E是弧BC的中点时,求△ADE的面积;
(2)若![]() ,求AE的长;
,求AE的长;
(3)点F是半径OC上一动点,设点E到直线OC的距离为m,当△DEF是等腰直角三角形时,求m的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)作EH⊥AB,连接OE,EB,设DH=a,则HB=2﹣a,OH=2+a,则EH=OH=2+a,根据Rt△AEB中,EH2=AHBH,即可求出a的值,即可求出S△ADE的值;
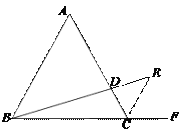
(2)作DF⊥AE,垂足为F,连接BE,设EF=2x,DF=3x,根据DF∥BE故![]() ,得出AF=6x,再利用Rt△AFD中,AF2+DF2=AD2,即可求出x,进而求出AE的长;
,得出AF=6x,再利用Rt△AFD中,AF2+DF2=AD2,即可求出x,进而求出AE的长;
(3)根据等腰直角三角形的不同顶点进行分类讨论,分别求出m的值.
解:(1)如图,作EH⊥AB,连接OE,EB,
设DH=a,则HB=2﹣a,OH=2+a,
∵点E是弧BC中点,
∴∠COE=∠EOH=45°,
∴EH=OH=2+a,
在Rt△AEB中,EH2=AHBH,
(2+a)2=(6+a)(2﹣a),
解得a=![]() ,
,
∴a=![]() ,
,
EH=![]() ,
,
S△ADE=![]() ;
;
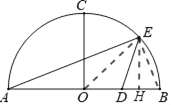
(2)如图,作DF⊥AE,垂足为F,连接BE

设EF=2x,DF=3x
∵DF∥BE
∴![]()
∴![]() =3
=3
∴AF=6x
在Rt△AFD中,AF2+DF2=AD2
(6x)2+(3x)2=(6)2
解得x=![]()
AE![]()
(3)当点D为等腰直角三角形直角顶点时,如图
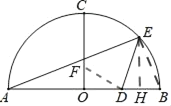
设DH=a
由DF=DE,∠DOF=∠EHD=90°,∠FDO+∠DFO=∠FDO+∠EDH,
∴∠DFO=∠EDH
∴△ODF≌△HED
∴OD=EH=2
在Rt△ABE中,EH2=AHBH
(2)2=(6+a)(2﹣a)
解得a=±![]()
m=![]()
当点E为等腰直角三角形直角顶点时,如图
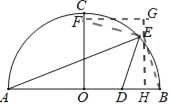
同理得△EFG≌△DEH
设DH=a,则GE=a,EH=FG=2+a
在Rt△ABE中,EH2=AHBH
(2+a)2=(6+a)(2﹣a)
解得a=![]()
∴m=![]()
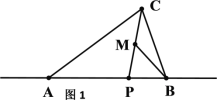
当点F为等腰直角三角形直角顶点时,如图
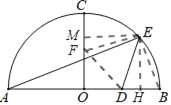
同理得△EFM≌△FDO
设OF=a,则ME=a,MF=OD=2
∴EH=a+2
在Rt△ABE中,EH2=AHBH
(a+2)2=(4+a)(4﹣a)
解得a=±![]()
m=![]()

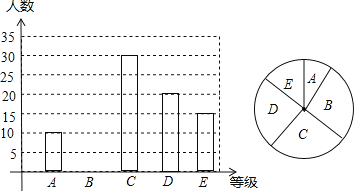
【题目】2019年,我省中考体育分值增加到55分,其中女生必考项目为八百米跑,我校现抽取九年级部分女生进行八百米测试成绩如下:
成绩 | 3′40″及以下 | 3′41~4′ | 4′01″~4′20′ | 4′21″~4′40″ | 4′41″及以上 |
等级 | A | B | C | D | E |
百分比 | 10% | 25% | m | 20% | n |
(1)求样本容量及表格中的m和n的值
(2)求扇形统计图中A等级所对的圆心角度数,并补全统计图.
(3)我校9年级共有女生500人.若女生八百米成绩的达标成绩为4分,我校九年级女生八百米成绩达标的人数有多少?