题目内容
【题目】在△ABC中,∠A=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
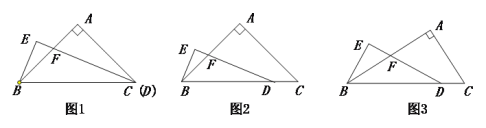
探究:当AB=AC且C,D两点重合时(如图1)探究:
(1)线段BE与FD之间的数量关系,直接写出结果 ;
(2)∠EBF= .
证明:当AB=AC且C,D不重合时,探究线段BE与FD的数量关系,并加以证明.
计算:当AB=![]() AC时,如图,求
AC时,如图,求![]() 的值 (用含
的值 (用含![]() 的式子表示).
的式子表示).
【答案】(1)BE=![]() FD;(2)22.5°,证明:BE=
FD;(2)22.5°,证明:BE=![]() FD,见解析;计算:
FD,见解析;计算:![]()
【解析】
探究:(1)首先延长CA与BE交于点G,根据∠EDB=![]() ∠C,BE⊥DE,判断出BE=EG=
∠C,BE⊥DE,判断出BE=EG=![]() BG;然后根据全等三角形的判定方法,判断出△ABG≌△ACF,即可判断出BG=CF=FD,再根据BE=
BG;然后根据全等三角形的判定方法,判断出△ABG≌△ACF,即可判断出BG=CF=FD,再根据BE=![]() BG,可得BE=
BG,可得BE=![]() FD,据此判断即可;
FD,据此判断即可;
(2)根据(1)的结论易求得答案;
证明:过点D作DG∥CA,与BE的延长线相交于点G,与AB相交于点H,仿照(1)的方法判断出△DEB≌△DEG和△GBH≌△FDH,即可推出结论;
计算:利用(2)的结论证得△GBH∽△FDH和△BHD∽△BAC,利用对应边成比例即可求得结论.
探究:(1)如图①,延长CA与BE交于点G,
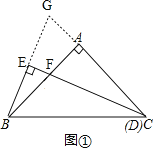
∵∠EDB=![]() ∠C,
∠C,
∴∠EDB =∠EDG,
即CE是∠BCG的平分线,
又∵BE⊥DE,
∴BE=EG=![]() BG,
BG,
∵∠BED=∠BAD=90°,∠BFE=∠CFA,
∴∠EBF=∠ACF,
即∠ABG=∠ACF,
在△ABG和△ACF中,
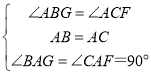 ,
,
∴△ABG≌△ACF,
∴BG=CF=FD,
又∵BE=![]() BG,
BG,
∴BE=![]() FD;
FD;
(2)∵AB=AC,∠A=90°,
∴∠ACB=45![]() ,
,
由(1)得CE是∠BCG的平分线,且∠EBF=∠ACF,
∴∠EBF=![]() ∠ACB=
∠ACB=![]() ;
;
证明:结论BE=![]() FD.
FD.
证明如下:
如图②,过点D作DG∥CA,与BE的延长线相交于点G,与AB相交于点H,
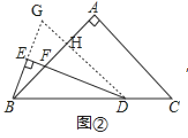
则∠GDB=∠C,∠BHD=∠A=90°=∠GHB.
∵∠EDB=![]() ∠C=
∠C=![]() ∠GDB=∠EDG,
∠GDB=∠EDG,
在△DEB和△DEG中,
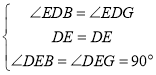 ,
,
∴△DEB≌△DEG,
∴BE=GE=![]() GB.
GB.
∵∠A=90°,AB=AC,
∴∠ABC=∠C=∠GDB,
∴HB=HD.
∵∠BED=∠BHD=90°, ∠BFE=∠DFH,
∴∠EBF=∠HDF,
在△GBH和△FDH中,
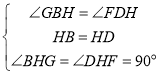 ,
,
∴△GBH≌△FDH,
∴GB=FD,
∴BE=![]() FD;
FD;
计算:∵△DEB≌△DEG,BE=![]() GB,∠BHD=∠BEF=90°,∠EBF=∠HDF,
GB,∠BHD=∠BEF=90°,∠EBF=∠HDF,
∴△GBH∽△FDH,
∴![]() ,即
,即![]() .
.
又∵DG∥CA,
∴△BHD∽△BAC,
∴![]() ,即
,即![]() .
.
∴![]() .
.

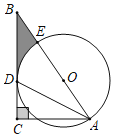
【题目】如图,Rt△ABC中,∠ACB=90°,AD平分∠BAC交BC于点D,点O为AB上一点,以O为圆心,AO为半径的圆经过点D.
(1)求证:BC与⊙O相切;
(2)若BD=AD=![]() ,求阴影部分的面积.
,求阴影部分的面积.
【题目】![]() 年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:
年新冠肺炎疫情发生以来,每天测体温成为一种制度,手持红外测温枪成为紧俏商品.某经销店承诺对所有商品明码标价,绝不哄抬物价.如下表所示是该店甲、乙两种手持红外测温枪的进价和售价:
商品 价格 | 甲 | 乙 |
进件(元 |
|
|
售价(元 |
|
|
该店有一批用![]() 元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共
元购进的甲、乙两种手持红外测温枪库存,预计全部销售后可获毛利润共![]() 元.[毛利润
元.[毛利润![]() (售价
(售价![]() 进价)
进价)![]() 销售量]
销售量]


(1)该店库存的甲、乙两种手持红外测温枪分别为多少个?
(2)根据销售情况,该店计划增加甲种手持红外测温枪的购进量,减少乙种手持红外测温枪的购进量.已知甲种手持红外测温枪增加的数量是乙种手持红外测温枪减少的数量的![]() 倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过
倍,进货价不变,而且用于购进这两种手持红外测温枪的总资金不超过![]() 元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润.
元,则该店怎样进货,可使全部销售后获得的毛利润最大?并求出最大毛利润.