题目内容
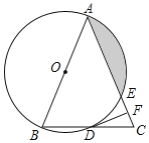
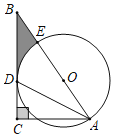
【题目】如图，Rt△ABC中，∠ACB＝90°，AD平分∠BAC交BC于点D，点O为AB上一点，以O为圆心，AO为半径的圆经过点D．
（1）求证：BC与⊙O相切；
（2）若BD＝AD＝
，求阴影部分的面积．
【答案】（1）详见解析；（2）
﹣
．
【解析】
（1）连接OD，通过证明DC⊥DO即可得解；
（2）根据题意，先算出
与扇形
的面积，再通过S△BDO -S扇形ODE即可得到阴影部分的面积.
（1）如下图，连接OD
∵AD平分∠BAC
∴∠BAD＝∠DAC
∵OD＝OA
∴∠ODA＝∠OAD
∵∠ODA＝∠DAC
∴OD∥AC
∴
∴DC⊥DO
∵DO为⊙O的半径
∴BC与⊙O相切；
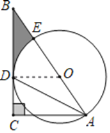
（2）∵
∴∠B＝∠DAB
∵∠BAD＝∠DAC
∴∠B＝∠BAD＝∠DAC
∵
∴
∴
在
中，BO＝2DO，
∵
∴DO＝1
∴
∴
∴阴影部分的面积＝
.
练习册系列答案
备战中考寒假系列答案
相关题目
