题目内容
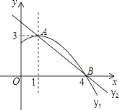
【题目】如图,在平面直角坐标系中,抛物线![]() 经过
经过![]() 三点,且
三点,且![]() .
.
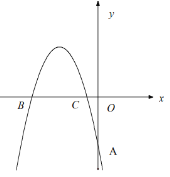
(1)求![]() 的值;
的值;
(2)在抛物线上求一点![]() 使得四边形
使得四边形![]() 是以
是以![]() 为对角线的菱形;
为对角线的菱形;
(3)在抛物线上是否存在一点![]() ,使得四边形
,使得四边形![]() 是以
是以![]() 为对角线的菱形?若存在,求出点
为对角线的菱形?若存在,求出点![]() 的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)D
;(2)D![]() ;(3)存在,
;(3)存在,![]() ,这个菱形不是正方形.
,这个菱形不是正方形.
【解析】
(1)把A(0,-4)代入可求c,运用两根关系及x2-x1=5,对式子合理变形,求b;
(2)因为菱形的对角线互相垂直平分,故菱形的另外一条对角线必在抛物线的对称轴上,满足条件的D点,就是抛物线的顶点;
(3)根据四边形BPOH是以OB为对角线的菱形,可得PH垂直平分OB,求出OB的中点坐标,代入抛物线解析式即可,再根据所求点的坐标与线段OB的长度关系,判断是否为正方形.
解:(1)![]() 抛物线
抛物线![]() 经过点
经过点![]()
![]()
又由题意可知,![]() 是方程
是方程![]() 的两个根,
的两个根,
![]() ,
,![]()
由已知得![]()
又![]()
![]()
![]()
解得![]() ,
,
当![]() 时,抛物线与
时,抛物线与![]() 轴的交点在
轴的交点在![]() 轴的正半轴上,不合题意,舍去.
轴的正半轴上,不合题意,舍去.
![]() ;
;
(2)∵四边形![]() 是以
是以![]() 为对角线的菱形,根据菱形的性质,点
为对角线的菱形,根据菱形的性质,点![]() 必在抛物线的对称轴上,
必在抛物线的对称轴上,
又![]()
![]() 拋物线的顶点
拋物线的顶点![]() 即为所求的点
即为所求的点![]() ;
;
(3)∵四边形![]() 是以
是以![]() 为对角线的菱形,点
为对角线的菱形,点![]() 的坐标为
的坐标为![]()
根据菱形的性质,
点![]() 必是直线
必是直线![]() 与抛物线
与抛物线![]() 的交点,
的交点,
![]() 当
当![]() 时,
时,![]()
![]() 在抛物线上存在一点
在抛物线上存在一点![]() ,使得四边形
,使得四边形![]() 为菱形.
为菱形.
四边形![]() 不能成为正方形,
不能成为正方形,
因为如果四边形![]() 为正方形,.点
为正方形,.点![]() 的坐标只能是
的坐标只能是![]() ,但这一点不在抛物线上.
,但这一点不在抛物线上.

练习册系列答案
相关题目