题目内容
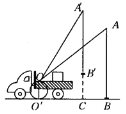
【题目】小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至 A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊绳A′B′=AB.AB垂直地面 O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA![]() ,sinA′
,sinA′![]() .求此重物在水平方向移动的距离BC.
.求此重物在水平方向移动的距离BC.
【答案】3
【解析】
作OD⊥AB于D,交A′C于E,根据余弦的定义求出AD,根据勾股定理求出OD,根据正弦的定义求出OE,结合图形计算得到答案.
如图,过点O作OD⊥AB于点D,交A′C于点E.
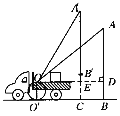
根据题意可知EC=DB=OO′=2,ED=BC,
∴∠A′EO=∠ADO=90°.
在Rt△AOD中,
∵cosA![]() ,OA=10,
,OA=10,
∴AD =6,
∴![]() .
.
在Rt△A′OE中,
∵![]() ,OA′=10.
,OA′=10.
∴OE=5.
∴BC=3.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目