题目内容
【题目】如图，抛物线L1：y=﹣x2+bx+c经过点A（1，0）和点B（5，0）已知直线l的解析式为y=kx﹣5．
（1）求抛物线L1的解析式、对称轴和顶点坐标．
（2）若直线l将线段AB分成1：3两部分，求k的值；
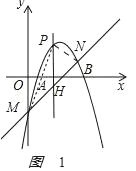
（3）当k=2时，直线与抛物线交于M、N两点，点P是抛物线位于直线上方的一点，当△PMN面积最大时，求P点坐标，并求面积的最大值．
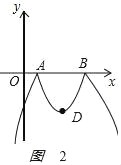
（4）将抛物线L1在x轴上方的部分沿x轴折叠到x轴下方，将这部分图象与原抛物线剩余的部分组成的新图象记为L2
①直接写出y随x的增大而增大时x的取值范围；
②直接写出直线l与图象L2有四个交点时k的取值范围．
【答案】（1）解析式为y=﹣x2+6x﹣5，对称轴：直线x=3，顶点坐标（3，4）；（2）k=
或k=
；（3）当x=2时，SPMN最大，最大值为8，此时P（2，3）；（4）①当x≤1或3≤x≤5时y随x的增大而增大；②当
＜k＜1时，直线l与图象L2有四个交点．
【解析】
（1）根据待定系数法，可得函数解析式；（2）根据线段的比，可得直线与x轴的交点，根据自变量与函数值的对应关系，可得答案；（3）根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标，可得PH，根据三角形的面积，可得二次函数，根据二次函数的性质，可得答案；（4）①根据函数图象的增减趋势，可得答案；②根据函数图象的交点，可得直线经过D，B点，根据自变量与函数值的对应关系，可得相应的k值，可得答案．
（1）∵抛物线L1：y=﹣x2+bx+c经过点A（1，0）和点B（5，0）
∴y=﹣（x﹣1）（x﹣5）=﹣（x﹣3）2+4，
∴抛物线L1的解析式为y=﹣x2+6x﹣5
对称轴：直线x=3
顶点坐标（3，4）；
（2）∵直线l将线段AB分成1：3两部分，则l经过点（2，0）或（4，0），
∴0=2k﹣5或0=4 k﹣5
∴k=或k=.
（3）如图1
，
设P（x，﹣x2+6x﹣5）是抛物线位于直线上方的一点，
解方程组
，解得
或
不妨设M（0，﹣5）、N（4，3）
∴0＜x＜4
过P做PH⊥x轴交直线l于点H，
则H（x，2x﹣5），
PH=﹣x2+6x﹣5﹣（2x﹣5）=﹣x2+4x，
S△PMN=
PHxN
=（﹣x2+4x）×4
=﹣2（x﹣2）2+8
∵0＜x＜4
∴当x=2时，SPMN最大，最大值为8，此时P（2，3）
（4）如图2
，
A（1，0），B（5，0）．由翻折，得D（3，﹣4），
①当x≤1或3≤x≤5时y随x的增大而增大
②当y=kx﹣5过D点时，3k﹣5=﹣4，解得k=，
当y=kx﹣5过B点时，5k﹣5=0，解得k=1，
直线与抛物线的交点在BD之间时有四个交点，即＜k＜1，
当＜k＜1时，直线l与图象L2有四个交点．
