Question

【题目】如图，在正方形ABCD中，O是对角线AC与BD的交点，M是BC边上的动点(点M不与点B，C重合)，过点C作CN⊥DM交AB于点N，连结OM、ON，MN．下列五个结论：①△CNB≌△DMC；②ON＝OM；③ON⊥OM；④若AB＝2，则S△OMN的最小值是1；⑤AN2+CM2＝MN2．其中正确结论是_____；(只填序号)

Answer 1

【答案】①②③⑤

【解析】

①由正方形的性质得出CD=BC，∠BCD=90°，证出∠BCN=∠CDM，由ASA即可得出结论；

②由全等三角形的性质得出CM=BN，由正方形的性质得出∠OCM=∠OBN=45°，OC=OB，由SAS证得△OCM≌△OBN（SAS）即可得出结论；

③由△OCM≌△OBN，得出∠COM=∠BON，则∠BOM+∠COM=∠BOM+∠BON，即可得出结论；

④由AB=2，得出S正方形ABCD=4，由△OCM≌△OBN得出四边形BMON的面积=△BOC的面积=1，即四边形BMON的面积是定值1，推出△MNB的面积有最大值即可得出结论；

⑤由CM=BN，BM=AN，由勾股定理即可得出结论．

①∵正方形ABCD中，CD＝BC，∠BCD＝90°，

∴∠BCN+∠DCN＝90°，

∵CN⊥DM，

∴∠CDM+∠DCN＝90°，

∴∠BCN＝∠CDM，

在△CNB和△DMC中

，

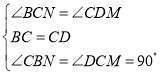∴△CNB≌△DMC(ASA)，

故①正确；

②∵△CNB≌△DMC，

∴CM＝BN，

∵四边形ABCD是正方形，

∴∠OCM＝∠OBN＝45°，OC＝OB，

在△OCM和△OBN中，

，

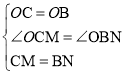∴△OCM≌△OBN(SAS)，

∴OM＝ON，

故②正确；

③∵△OCM≌△OBN，

∴∠COM＝∠BON，

∴∠BOM+∠COM＝∠BOM+∠BON，即∠NOM＝∠BOC＝90°，

∴ON⊥OM；

故③正确；

④∵AB＝2，

∴S正方形ABCD＝4，

∵△OCM≌△OBN，

∴四边形BMON的面积＝△BOC的面积＝1，即四边形BMON的面积是定值1，

∴当△MNB的面积最大时，△MNO的面积最小，

设BN＝x＝CM，则BM＝2﹣x，

∴△MNB的面积S＝x(2﹣x)＝﹣x2+x＝﹣(x﹣1)2+，

∴当x＝1时，△MNB的面积有最大值，

此时S△OMN的最小值是1﹣＝，

故④不正确；

⑤∵AB＝BC，CM＝BN，

∴BM＝AN，

在Rt△BMN中，BM2+BN2＝MN2，

∴AN2+CM2＝MN2，

故⑤正确；

∴本题正确的结论有：①②③⑤，

故答案为①②③⑤．