题目内容
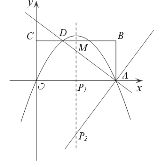
【题目】矩形OABC在平面直角坐标系中的位置如图所示,A、C两点的坐标分别为A(6,0)、C(0,3),直线![]() 与BC边相交于点D.
与BC边相交于点D.

(1)求点D的坐标;
(2)若抛物线![]() 经过A、D两点,试确定此抛物线的解析式;
经过A、D两点,试确定此抛物线的解析式;
(3)设(2)中的抛物线的对称轴与直线AD交于点M,点P为对称轴上一动点,以P、A、M为顶点的三角形与△ABD相似,求符合条件的所有点P的坐标.
【答案】(1)点D的坐标为(2,3);
(2) 抛物线的解析式为![]() ;
;
(3) 符合条件的点P有两个,P1 (3,0)、P2 (3,-4).
【解析】
试题分析:(1)有题目所给信息可以知道,BC线上所有的点的纵坐标都是3,又有D在直线![]() 上,代入后求解可以得出答案.
上,代入后求解可以得出答案.
(2)A、D,两点坐标已知,把它们代入二次函数解析式中,得出两个二元一次方程,联立求解可以得出答案.
(3)由题目分析可以知道∠B=90°,以P、A、M为顶点的三角形与△ABD相似,所以应有∠APM、∠AMP或者∠MAP等于90°,很明显∠AMP不可能等于90°,所以有两种情况.
解:(1) ∵四边形OABC为矩形,C(0,3)
∴BC∥OA,点D的纵坐标为3.
∵直线![]() 与BC边相交于点D,
与BC边相交于点D,
∴![]() . ∴点D的坐标为(2,3).
. ∴点D的坐标为(2,3).
(2) ∵若抛物线![]() 经过A(6,0)、D(2,3)两点,
经过A(6,0)、D(2,3)两点,
∴![]()
解得: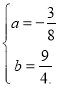 ∴抛物线的解析式为
∴抛物线的解析式为![]()
(3) ∵抛物线![]() 的对称轴为x=3,
的对称轴为x=3,
设对称轴x=3与x轴交于点P1,∴BA∥MP1,
∴∠BAD=∠AMP1.
①∵∠AP1M=∠ABD=90°,∴△ABD∽△AMP1.
∴P1 (3,0).
②当∠MAP2=∠ABD=90°时,△ABD∽△MAP2.
∴∠AP2M=∠ADB
∵AP1=AB,∠AP1 P2=∠ABD=90°
∴△AP1 P2≌△ABD
∴P1 P2=BD=4
∵点P2在第四象限,∴P2 (3,-4).
∴符合条件的点P有两个,P1 (3,0)、P2 (3,-4).

 阅读快车系列答案
阅读快车系列答案【题目】自行车每节链条的长度为2.5 cm,交叉重叠部分的圆的直径为0.8 cm.

(1)观察图形,填写下表:
链条的节数/节 | 2 | 3 | 4 | … |
链条的长度/cm | … |
(2)如果x节链条的长度为y(cm),那么y与x之间的关系式是什么?
(3)如果一辆某种型号自行车的链条(安装前)由60节这样的链条组成,那么这辆自行车上的链条(安装后)总长度是多少?