题目内容
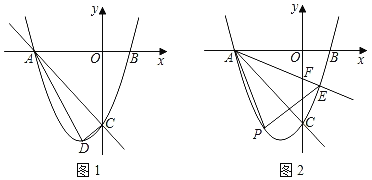
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 若点
若点![]() 为第一象限抛物线上一点,连接
为第一象限抛物线上一点,连接![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() ,得到线段
,得到线段![]() 连接
连接![]() 过点
过点![]() 作直线
作直线![]() 的垂线,垂足为点E,过点
的垂线,垂足为点E,过点![]() 作直线
作直线![]() 的垂线,垂足为点
的垂线,垂足为点![]() ,作线段
,作线段![]() 的垂直平分线交
的垂直平分线交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
![]() 在
在![]() 的条件下,延长
的条件下,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,当
,当![]() 时,求
时,求![]() 的正切值.
的正切值.
【答案】(1) ![]() ; (2) D(1,4); (3)
; (2) D(1,4); (3)![]()
【解析】
(1)可用k表示点C的坐标,利用OA和OC线段长的关系,得出点A的坐标,代入解析式求解即可;
(2)根据解析式,可求得A、B的坐标,根据![]() 以及GH垂直平分EF,可得
以及GH垂直平分EF,可得![]() ,进而得出H的坐标,最后确定D的坐标;
,进而得出H的坐标,最后确定D的坐标;
(3)如下图,设![]() ,联立直线PA和抛物线的解析式,计算可得PA的解析式,同理得PB的解析式,根据MD=NH可推得
,联立直线PA和抛物线的解析式,计算可得PA的解析式,同理得PB的解析式,根据MD=NH可推得![]() ,求tan∠BPK即可.
,求tan∠BPK即可.
(1)解:当![]() 时,
时,![]()
解得![]()
![]()
![]()
![]()
![]()
![]()
![]() 点
点![]() 在抛物线上
在抛物线上
![]()
解得![]() (舍),
(舍),![]()
![]() 抛物线的解析式为
抛物线的解析式为![]()
(2)解:![]() 抛物线的解析式为
抛物线的解析式为![]()
![]() 当
当![]() 时,
时,![]()
解得![]()
![]()
![]()
![]()
如下图:
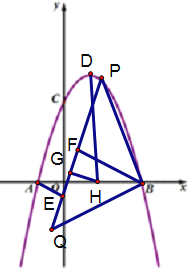
![]()
![]()
![]()
![]() 垂直平分
垂直平分![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 轴
轴
![]() 点
点![]() 的横坐标为
的横坐标为![]()
![]() 当
当![]() 时,
时,![]()
(3)过![]() 作
作![]() 于
于![]() ,
,

∵点![]() 在抛物线
在抛物线![]() 上
上
设![]()
由(2)知![]() ,
,
设直线![]() 的解析式为
的解析式为![]()
点![]() 在直线
在直线![]() 上,
上,
则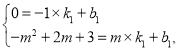
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]() 的横坐标为
的横坐标为![]()
![]() 当
当![]() 时,
时,![]()
![]()
设直线![]() 的解析式为
的解析式为![]()
点![]() 在直线
在直线![]() 上
上
则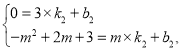
解得![]()
![]() 直线
直线![]() 的解析式为
的解析式为![]()
![]() 的横坐标为
的横坐标为![]()
![]() 当
当![]() 时,
时,![]()
![]()
![]()
![]()
![]()
![]()
![]()
解得![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
即![]()
在![]() 中,
中,![]()
![]()

练习册系列答案
相关题目