题目内容
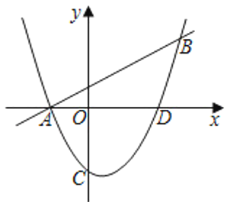
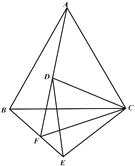
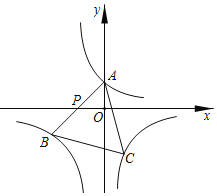
【题目】如图,将反比例函数y=![]() (k>0)的图象向左平移2个单位长度后记为图象c,c与y轴相交于点A,点P为x轴上一点,点A关于点P的对称点B在图象c上,以线段AB为边作等边△ABC,顶点C恰好在反比例函数y=﹣
(k>0)的图象向左平移2个单位长度后记为图象c,c与y轴相交于点A,点P为x轴上一点,点A关于点P的对称点B在图象c上,以线段AB为边作等边△ABC,顶点C恰好在反比例函数y=﹣![]() (x>0)的图象上,则k=_____.
(x>0)的图象上,则k=_____.
【答案】2![]() .
.
【解析】
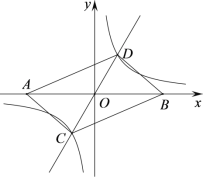
如图,连接PC,过C作CH⊥x轴于H.利用相似三角形的性质表示出点C的坐标,再利用待定系数法解决问题即可.
如图,连接PC,过C作CH⊥x轴于H.
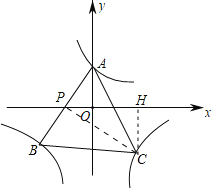
由题意A(0,![]() ),P(﹣2,0),B(﹣4,﹣
),P(﹣2,0),B(﹣4,﹣![]() ),
),
∴△ABC是等边三角形,PA=PB,
∴PC⊥AB,∠ACP=∠BCP=30°,
∴PC=![]() PA,
PA,
∴∠APC=∠AOP=∠PHC=90°,
∴∠APO+∠CPH=90°,∠CPH+∠PCH=90°,
∴∠APO=∠PCH,
∴△AOP∽△PHC,
∴![]() .
.
∴PH=![]() k,CH=2
k,CH=2![]() ,
,
∴OH=![]() k﹣2,
k﹣2,
∴C(![]() k﹣2,﹣2
k﹣2,﹣2![]() ),
),
∵点C在y=﹣![]() 上,
上,
∴﹣2![]() (
(![]() k﹣2)=﹣k,
k﹣2)=﹣k,
解得k=2![]() ,
,
故答案为2![]() .
.

练习册系列答案
相关题目