题目内容
一条河的两岸有一段是平行的.在河的这一岸每相距5米在一棵树,在河的对岸每相距50米在一根电线杆.在这岸离开岸边25米处看对岸,看到对岸相邻的两根电线杆恰好被这岸的两棵树遮住,并且在这两棵树之间还有三棵树,求河宽.


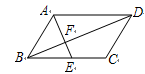
如图,
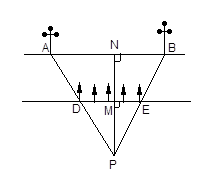
由题知AB=50,DE=20,PM=25;
因DE∥AB,
∴ΔPDE∽ΔPAB,
从而PM∶PN=DE∶AB,
设MN=x米,则25∶(25+x)=20∶50,
x=37.5(米)
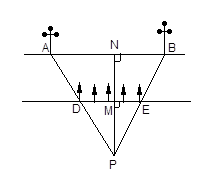
由题知AB=50,DE=20,PM=25;
因DE∥AB,
∴ΔPDE∽ΔPAB,
从而PM∶PN=DE∶AB,
设MN=x米,则25∶(25+x)=20∶50,
x=37.5(米)
画出图形,找出题中的相似三角形,根据相似三角形的性质即可解答.

练习册系列答案
相关题目
 ,则
,则

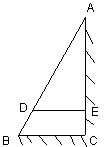
 中,
中,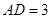 厘米,
厘米,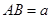 厘米(
厘米(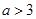 ).动点
).动点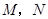 同时从
同时从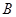 点出发,分别沿
点出发,分别沿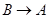 ,
,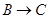 运动,速度是
运动,速度是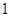 厘米/秒.过
厘米/秒.过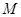 作直线垂直于
作直线垂直于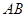 ,分别交
,分别交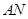 ,
,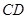 于
于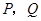 .当点
.当点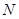 到达终点
到达终点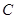 时,点
时,点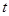 秒.
秒.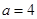 厘米,
厘米,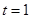 秒,则
秒,则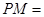 ______厘米;
______厘米;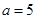 厘米,求时间
厘米,求时间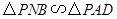 ,并求出它们的相似比;
,并求出它们的相似比;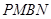 与梯形
与梯形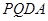 的面积相等,求
的面积相等,求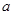 的取值范围;
的取值范围;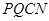 的面积都相等?若存在,求
的面积都相等?若存在,求