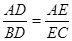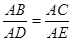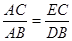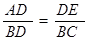题目内容
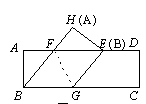
如图,矩形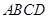 中,
中, 厘米,
厘米,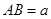 厘米(
厘米(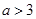 ).动点
).动点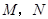 同时从
同时从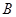 点出发,分别沿
点出发,分别沿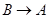 ,
,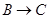 运动,速度是
运动,速度是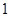 厘米/秒.过
厘米/秒.过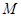 作直线垂直于
作直线垂直于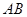 ,分别交
,分别交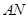 ,
,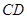 于
于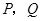 .当点
.当点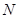 到达终点
到达终点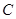 时,点
时,点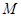 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为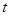 秒.
秒.
(1)若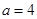 厘米,
厘米,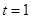 秒,则
秒,则 ______厘米;
______厘米;
(2)若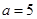 厘米,求时间
厘米,求时间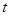 ,使
,使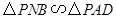 ,并求出它们的相似比;
,并求出它们的相似比;
(3)若在运动过程中,存在某时刻使梯形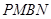 与梯形
与梯形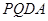 的面积相等,求
的面积相等,求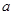 的取值范围;
的取值范围;
(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形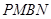 ,梯形
,梯形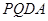 ,梯形
,梯形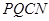 的面积都相等?若存在,求
的面积都相等?若存在,求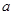 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.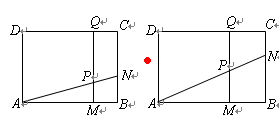
 中,
中, 厘米,
厘米,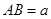 厘米(
厘米(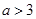 ).动点
).动点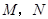 同时从
同时从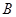 点出发,分别沿
点出发,分别沿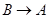 ,
,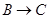 运动,速度是
运动,速度是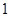 厘米/秒.过
厘米/秒.过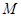 作直线垂直于
作直线垂直于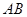 ,分别交
,分别交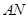 ,
,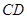 于
于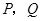 .当点
.当点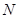 到达终点
到达终点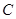 时,点
时,点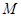 也随之停止运动.设运动时间为
也随之停止运动.设运动时间为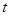 秒.
秒.(1)若
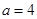 厘米,
厘米,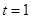 秒,则
秒,则 ______厘米;
______厘米;(2)若
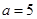 厘米,求时间
厘米,求时间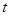 ,使
,使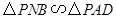 ,并求出它们的相似比;
,并求出它们的相似比;(3)若在运动过程中,存在某时刻使梯形
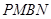 与梯形
与梯形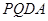 的面积相等,求
的面积相等,求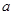 的取值范围;
的取值范围;(4)是否存在这样的矩形:在运动过程中,存在某时刻使梯形
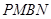 ,梯形
,梯形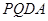 ,梯形
,梯形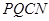 的面积都相等?若存在,求
的面积都相等?若存在,求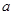 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)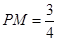 ,
,
(2)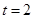 ,使
,使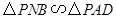 ,相似比为
,相似比为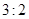
(3)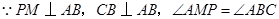 ,
,
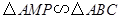 ,
,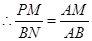 即
即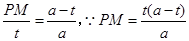 ,
,
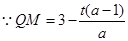
当梯形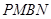 与梯形
与梯形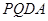 的面积相等,即
的面积相等,即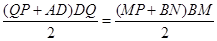
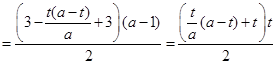 化简得
化简得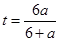 ,
,
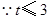 ,
,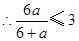 ,则
,则 ,
,
(4) 时,梯形
时,梯形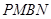 与梯形
与梯形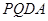 的面积相等
的面积相等
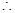 梯形
梯形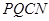 的面积与梯形
的面积与梯形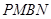 的面积相等即可,则
的面积相等即可,则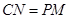
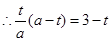 ,把
,把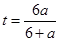 代入,解之得
代入,解之得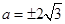 ,所以
,所以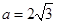 .
.
所以,存在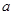 ,当
,当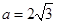 时梯形
时梯形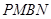 与梯形
与梯形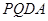 的面积、梯形
的面积、梯形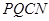 的面积相等.
的面积相等.
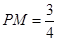 ,
,(2)
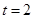 ,使
,使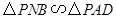 ,相似比为
,相似比为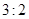
(3)
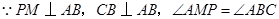 ,
,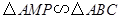 ,
,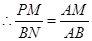 即
即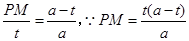 ,
,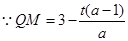
当梯形
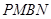 与梯形
与梯形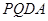 的面积相等,即
的面积相等,即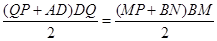
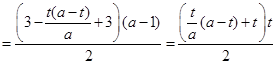 化简得
化简得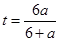 ,
,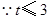 ,
,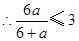 ,则
,则 ,
,(4)
 时,梯形
时,梯形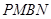 与梯形
与梯形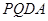 的面积相等
的面积相等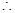 梯形
梯形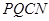 的面积与梯形
的面积与梯形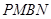 的面积相等即可,则
的面积相等即可,则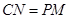
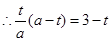 ,把
,把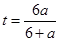 代入,解之得
代入,解之得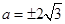 ,所以
,所以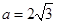 .
.所以,存在
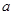 ,当
,当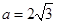 时梯形
时梯形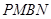 与梯形
与梯形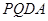 的面积、梯形
的面积、梯形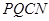 的面积相等.
的面积相等.(1)容易知道△ANB∽△APM,利用相似三角形的对应边成比例就可以求出PM;
(2)若PNB∽△PAD,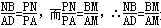 这样就可以求出t,也可以求出相似比;
这样就可以求出t,也可以求出相似比;
(3)首先利用△AMP∽△ABN把QM,PM用t表示,然后就可以用t表示梯形PMBN与梯形PQDA的面积,根据已知可以得到关于t的方程,最后就可以根据t与a的关系式就可以讨论t的取值范围了;
(4)根据(3)已经得到t的取值范围,再根据梯形PQCN的面积与梯形PMBN的面积相等得到关于t的方程,求出t,再求出a,这样就可以判断a的值是否存在
(2)若PNB∽△PAD,
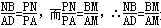 这样就可以求出t,也可以求出相似比;
这样就可以求出t,也可以求出相似比;(3)首先利用△AMP∽△ABN把QM,PM用t表示,然后就可以用t表示梯形PMBN与梯形PQDA的面积,根据已知可以得到关于t的方程,最后就可以根据t与a的关系式就可以讨论t的取值范围了;
(4)根据(3)已经得到t的取值范围,再根据梯形PQCN的面积与梯形PMBN的面积相等得到关于t的方程,求出t,再求出a,这样就可以判断a的值是否存在

练习册系列答案
相关题目
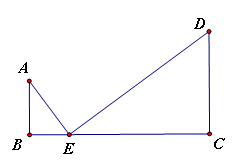
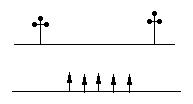

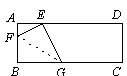
 。(说明:顶点都在网格线交点处的三角形叫做格点三角形。友情提示:请在画出的三角形的项点处标上相对应的字母!)
。(说明:顶点都在网格线交点处的三角形叫做格点三角形。友情提示:请在画出的三角形的项点处标上相对应的字母!)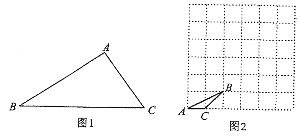
 中,
中,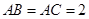 ,
,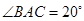 .动点
.动点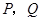 分别在直线
分别在直线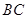 上运动,且始终保持
上运动,且始终保持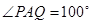 .设
.设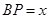 ,
,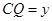 ,则
,则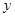 与
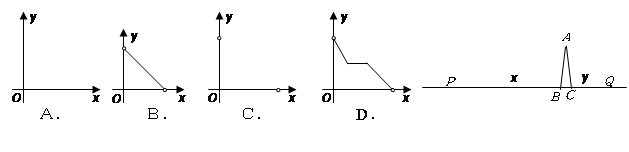
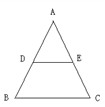
与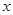 之间的函数关系用图象大致可以表示为( )
之间的函数关系用图象大致可以表示为( )