题目内容
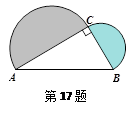
. 如图，△ABC中，∠ACB=90°，AB=6，分别以边AC、BC为直径向形外作两个半圆，则这两个半圆的面积的和为 ． （结果中保留π）
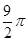. 根据半圆面积公式结合勾股定理，知S1+S2等于以斜边为直径的半圆面积．
解：∵以AB为直径大半圆的面积=
π×32=
，
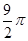所以这两个半圆的面积的和为=．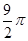
故答案为：．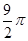
根据半圆的面积公式以及勾股定理证明：以直角三角形的两条直角边为直径的半圆面积和等于以斜边为直径的圆面积，重在验证勾股定理．
解：∵以AB为直径大半圆的面积=
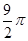π×32=，所以这两个半圆的面积的和为=
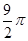．故答案为：
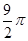．根据半圆的面积公式以及勾股定理证明：以直角三角形的两条直角边为直径的半圆面积和等于以斜边为直径的圆面积，重在验证勾股定理．
练习册系列答案
名校课堂系列答案
相关题目
直径AB是河底线，弦CD是水位线，CD∥AB，且CD =" 24" 
m．已测得水面距桥洞最高处有8m
中点到CD的距离）
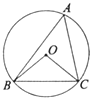
上，AO∥BC，∠OBC=40°，则∠ACB的度数是
