题目内容
【题目】如图, ![]() 为⊙
为⊙![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,点
,点![]() 是
是![]() 上一点,连结
上一点,连结![]() ,
, ![]() .
.
(![]() )在下添辅助线的前提下直接写出图中与
)在下添辅助线的前提下直接写出图中与![]() 相等的角,不用证明.
相等的角,不用证明.
(![]() )求证:当
)求证:当![]() 时,
时, ![]() 与
与![]() 相似.
相似.
(![]() )若
)若![]() ,求
,求![]() 的度数.
的度数.
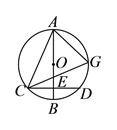
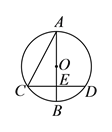
【答案】(1)![]() ;(2)答案见解析;(3)60°.
;(2)答案见解析;(3)60°.
【解析】试题分析:(1)结论:∠ACE=∠AGC.首先证明AB垂直平分CD,推出AC=AD,∠ACD=∠ADC,因为∠AGC=∠ADC,由此即可证明.
(2)如图2中,由DG∥AB,推出∠AEC=∠CDG=90°,推出CG是直径,推出∠CAG=90°,由此即可证明.
(3)如图3中,连接OC、BC.只要证明△OBC是等边三角形即可解决问题.
试题解析:解:(![]() )结论:∠ACE=∠AGC.理由如下:
)结论:∠ACE=∠AGC.理由如下:
如图1中,连接AD.
∵AB是直径,AB⊥CD,∴EC=ED,∴AD=AC,∴∠ACE=∠ADC.
∵∠AGC=∠ADC,∴∠ACE=∠AGC.
(![]() )证明:∵
)证明:∵![]() ,
,
∴![]() ,
,
∴![]() 也是直径,
也是直径,
∴![]() ,
, ![]() ,
,
∴![]() .
.
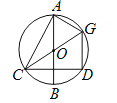
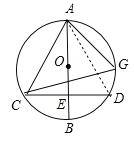
(![]() )如图,连接
)如图,连接![]() ,
, ![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目