Question

【题目】如图，点B、C分别在函数的图像上，AB∥x轴，AC∥y轴，已知点A的坐标为(2，m)()，延长OA交反比例函数的图像交于点P，

(1)当点P横坐标为3，求m的值；

(2)连接CO，当AC=OA时，求m的值；

(3)连接BP、CP，的值是否随m的变化而变化？若变化，说明理由；若不变，求出的值．

Answer 1

【答案】(1)；(2) ；(3) 不变，比值为1,理由见解析

【解析】

（1）先求出P的坐标为，再根据即可求出m的值；

（2）通过A点的坐标先求出C点的坐标，再根据即可求出m的值；

（3）通过反比例函数k的几何意义及三角形面积的求法进行求解即可得解.

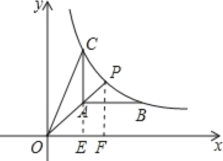
（1）延长CA交x轴于点E，过点P作轴于点F，则，如下图所示

∵点P在函数的图像上，且横坐标为3

∴点P的坐标为

∵

∴

∴，即

∴；

（2）∵，可求得

∴，

∵

∴

解得：；

（3）的值不变；

如下图，延长BA交轴于点M，延长CA交轴于点N，连接OB

易得

∵四边形AMON为矩形

∴

∴

∵，

∴

∴=1.