题目内容
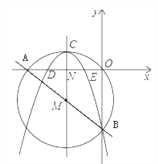
【题目】如图，在正方形网格图中建立平面直角坐标系，一条圆弧经过网格点A(0，4)、B(-4，4)、C(-6，2)，请在网格图中进行如下操作：
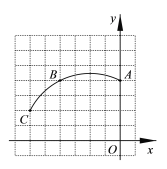
（1）利用网格图确定该圆弧所在圆的圆心D的位置（保留画图痕迹）；
（2）连接AD、CD，则⊙D的半径为_ __(结果保留根号)，∠ADC的度数为_ __；
（3）若扇形DAC是一个圆锥的侧面展开图，求该圆锥底面半径．(结果保留根号)．
【答案】(1)详见解析；(2)
，90°；(3) 
.
【解析】
(1)利用垂径定理得出
点位置即可；(2)利用点的坐标结合勾股定理得出⊙D的半径长，再利用全等三角形的判定与性质得出
的度数；(3)利用圆锥的底面圆的周长等于侧面展开图的扇形弧长即可得出结论.
解：(1)如图所示：作
的中垂线，交点即为所求，坐标为：
；
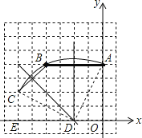
故答案为：(-2，0)；
(2)∵
，
，
∴
，
，
∴
，
即
的半径长为，
∵C(-6，2)，
∴EC=2，DE=4，
∴
，
∴在
和
中，
，
∴≌
)，
∴
，
，
∴
，
∴
，
故答案为：，90°；
(3)设圆锥的底面圆的半径为
，根据题意得出：
，
解得：
，
故答案为：.
练习册系列答案
相关题目
【题目】我市举行八年级“生活中的数学知识”竞赛活动，甲、乙两校分别派五名同学参加竞赛，其成绩分别是（单位：分）：甲校五名同学：
，
，
，，
；乙校五名同学：，
，
，，
．根据以上数据解答下列问题：
把表格空格填完整：
学校 | 平均数（分） | 中位数（分） | 众数（分） |
甲校五位同学 | ________ |
| ________ |
乙校五位同学 |
| ________ |
|
根据上述数据，请你分析哪所学校同学的竞赛成绩相对较好？
