Question

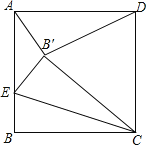
【题目】如图，正方形ABCD中，AB＝2，点E是AB上一点，将正方形沿CE折叠，点B落在正方形内一点B'处，若△AB'D为等腰三角形，则BE的长度为_____．

Answer 1

【答案】4﹣2或．

【解析】

由四边形ABCD是正方形，得到AB＝BC＝CD＝AD，因为△AB'D为等腰三角形，分三种情况：①AD＝B′D；②AB′＝B′D③AB′＝AD，分别进行讨论即可得出答案．

解：∵四边形ABCD是正方形，

∴AB＝BC＝CD＝AD，

①当AD＝B′D时，如图1，

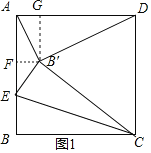
由折叠的性质得，B′C＝BC，

∴B′D＝B′C＝CD，

∴△CDB′是等边三角形，

∴∠B′DC＝60°，

∴∠ADB′＝30°，

过B′作B′G⊥AD于G，B′F⊥AB于F，

∴AF＝B′G＝=×2＝1，DG＝= ，

∴AG＝FB′＝2﹣，

∵BE＝B′E，EF＝1﹣BE，

∴（2﹣）2+（1﹣BE）2＝BE2，

∴BE＝4﹣2；

②当AB′＝B′D时，如图2，

则B′在AD的垂直平分线上，

∴B′在BC的垂直平分线上，

∴BB′＝CB′，

由折叠的性质得，B′C＝BC，

∴△BB′C是等边三角形，

∴∠BCE＝30°，

∴BE＝BC＝，

③当AB′＝AD时，则AB＝AB′，

∵EB＝EB′，CB＝CB′，

∴点E、C在BB′的垂直平分线上，

∴EC垂直平分BB′，

∴A与E重合，

∴B′与D重合，不符合题意，舍去．

综上所述，BE的长为4﹣2或．

故答案为：4﹣2或．