Question

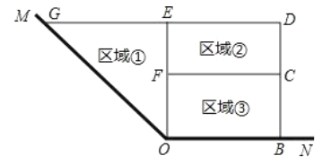
【题目】如图，在四边形中，，，，，点从点出发，以每秒的速度沿折线方向运动，点从点出发，以每秒的速度沿线段方向向点运动、已知动点，同时出发，当点运动到点时，点，停止运动，设运动时间为秒，在这个运动过程中，若的面积为，则满足条件的的值有（ ）

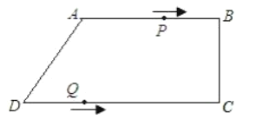
A.1个B.2个C.3个D.4个

Answer 1

【答案】B

【解析】

此题要分三种情况进行讨论：即①当点P在线段AB上，②当点P在线段BC上，③当点P在线段CD上，根据三种情况点的位置，可以确定t的值．

过点A作AM⊥CD于M，

根据勾股定理，AD=10cm，AM=BC=8cm，

∴DM==6（cm），

∴CD=16cm；

①当点P在线段AB上时，即0≤t≤时，如图：

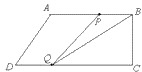
S△BPQ＝BPBC＝ (103t)×8＝20，

∴t＝；

当点P在线段BC上时，即＜t≤6时，如图：

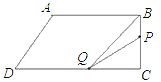
BP=3t-10，CQ=16-2t，

∴S△BPQ＝BPCQ＝ (3t10)×(162t)＝20，

化简得：3t2-34t+100=0，△=-44＜0，所以方程无实数解；

当点P在线段CD上时，

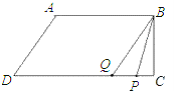
若点P在Q的右侧，即6＜t＜，

则有PQ=34-5t，

S△BPQ=（34-5t）×8=20，

t＝＜6，舍去，

若点P在Q的左侧，

即＜t≤8，

则有PQ=5t-34，S△BPQ＝ (5t34)×8＝20，

t=7.8，

综合得，满足条件的t存在，其值分别为t1＝，t2=7.8．

故选：B