题目内容
【题目】在圆![]() 中,弦
中,弦![]() 与弦
与弦![]() 相交于点
相交于点![]() ,
,![]() 于点
于点![]() ,过点
,过点![]() 作圆
作圆![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)如图①,若![]() ,求
,求![]() 的大小;
的大小;
(2)如图②,连接![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
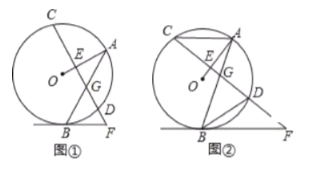
【答案】(1) ![]() ;(2)
;(2) ![]()
【解析】
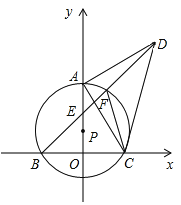
(1)如图①,连接OB,先利用切线的性质得∠OBF=90°,而OA⊥CD,所以∠OED=90°,利用四边形内角和可计算出∠AOB=130°,然后根据等腰三角形性质和三角形内角和计算出∠OBA=∠A=25°,从而得到∠GBF=65°;
(2)如图②,连接OB,BO的延长线交AC于H,利用切线的性质得OB⊥BF,再利用AC∥BF得到BH⊥AC,与(1)方法可得到∠AOB=144°,从而得到∠OBA=∠OAB=18°,接着计算出∠GBF.
(1)如图①,连接![]()
∵![]() 为
为![]() 的切线
的切线
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
又∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
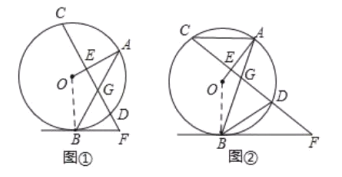
(2)由(1)知,![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]()
(本题条件多余,未用到![]() ,加上这个条件,可以得出
,加上这个条件,可以得出![]() )
)

练习册系列答案
相关题目