题目内容

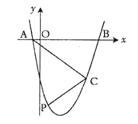
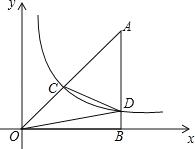
【题目】如图，△OAB中，∠ABO＝90°，点A位于第一象限，点O为坐标原点，点B在x轴正半轴上，若双曲线y＝（x＞0）与△OAB的边AO.AB分别交于点C.D，点C为AO的中点，连接OD.CD．若S△OBD＝3，则S△OCD为_____．

【答案】

【解析】

利用△OBD的面积求得反比例函数的比例系数k,从而求得△OCE的面积，然后根据三角形中线分三角形成面积相等的两个三角形，求得△OCD与△OAD的面积关系，从而求解

过点C作CE⊥x轴，交x轴于点E

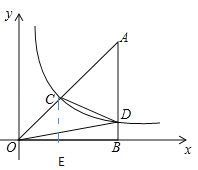
设D（x,y）,则S△OBD=

∴xy=6,即y=

设C（x,y）,则S△OCE=

又∵点C为AO的中点

∴

∴S△OAB=12,则S△AOD=12-3=9

又∵点C为AO的中点

∴S△OCD=

故答案为：.

练习册系列答案
相关题目

【题目】如图，四边形ABCD中，AD∥BC，点E是边AD的中点，连接BE并延长交CD的延长线于点F，交AC于点G.

(1)若FD＝2， ，求线段DC的长；

(2)求证：EF·GB＝BF·GE.

【题目】如图，抛物线为常数）交轴于两点.

（1）求抛物线的解析式；

（2）直接写出：①抛物线的顶点坐标；

②抛物线与轴交点关于该抛物线对称轴对称的点的坐标；

（3）在直线下方的抛物线上是否存在点使的面积最大？若存在，请求出点的坐标；若不存在，请说明理由.

【题目】如图，在Rt△ABC中，∠ACB=90°，点D是AB上的一点，连接CD，CE∥AB，BE∥CD，且CE=AD.

(1)求证：四边形BDCE是菱形；

(2)过点E作EF⊥BD，垂足为点F，若点F是BD的中点，EB=6，求BC的长.

【题目】“五一”期间，小华和妈妈到某景区游玩，小明想利用所学的数学知识，估测景区里的观景塔的高度，他从点处的观景塔出来走到点处.沿着斜坡从点走了米到达点，此时回望观景塔，更显气势宏伟.在点观察到观景塔顶端的仰角为且,再往前走到处，观察到观景塔顶端的仰角，测得之间的水平距离米，则观景塔的高度约为( ) 米. ()

A.B.C.D.

【题目】如图，已知抛物线y＝ax2+bx+5与x轴交于A（﹣1，0），B（5，0）两点（点A在点B的左侧），与y轴交于点C．

（1）求抛物线的解析式；

（2）点D是第一象限内抛物线上的一个动点（与点C，B不重合），过点D作DF⊥x轴于点F，交直线BC于点E，连接BD，直线BC能否把△BDF分成面积之比为2：3的两部分？若能，请求出点D的坐标；若不能，请说明理由．

（3）若M为抛物线对称轴上一动点，使得△MBC为直角三角形，请直接写出点M的坐标．

【题目】如图，P是抛物线y＝x2﹣4x+3上的一点，以点P为圆心、1个单位长度为半径作⊙P，当⊙P与直线y＝0相切时，点P的坐标为_____．

【题目】如图，在四边形中，，，，，点从点出发，以每秒的速度沿折线方向运动，点从点出发，以每秒的速度沿线段方向向点运动、已知动点，同时出发，当点运动到点时，点，停止运动，设运动时间为秒，在这个运动过程中，若的面积为，则满足条件的的值有（ ）

A.1个B.2个C.3个D.4个

【题目】在△ABC中，已知AB＝2，∠B＝30°，AC＝．则S△ABC＝_________.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网