题目内容
【题目】为了节省材料,某水产养殖户利用水库的一角![]() 两边为边,用总长为
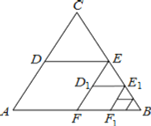
两边为边,用总长为![]() 的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且这三块区域的面积相等,四边形
的围网在水库中围成了如图所示的①②③三块区域,其中区域①为直角三角形,区域②③为矩形,而且这三块区域的面积相等,四边形![]() 为直角梯形.
为直角梯形.
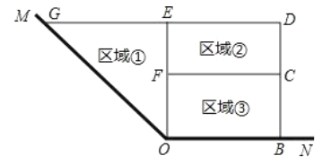
(1)设![]() 的长度为
的长度为![]() ,则
,则![]() 的长为______
的长为______![]() ;
;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并注明自变量
之间的函数关系式,并注明自变量![]() 的取值范围;
的取值范围;
(3)![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)当
;(3)当![]() 时,
时,![]() 有最大值,最大值是675平方米.
有最大值,最大值是675平方米.
【解析】
(1)根据三角形和矩形的面积得到![]() EGOE=CFEF=CFOF,得到EG=DE=CF=OB=x,于是得到结论;
EGOE=CFEF=CFOF,得到EG=DE=CF=OB=x,于是得到结论;
(2)由(1)知OE+DB=120-4x,得到OE=DB=60-2x,根据矩形的面积公式即可得到结论;
(3)把y=-3x2+90x配方得到y=-3(x-15)2+675,根据二次函数的性质即可得到结论.
(1)由题意得,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:![]() ;
;
(2)由(1)知![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
(3)∵![]() ,
,
∵![]() ,且
,且![]() ,
,
∴抛物线开口向下,
∴当![]() 时,
时,![]() 有最大值,最大值是675平方米.
有最大值,最大值是675平方米.

练习册系列答案
相关题目