Question

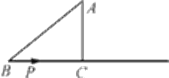
【题目】如图，在△ABC中，∠B＝2∠C，AD⊥BC于D，设AD＝b，BD＝a，则DC＝_____．(用含a，b的代数式表示)

Answer 1

【答案】

【解析】

在DC上取DE＝BD，然后根据线段垂直平分线上的点到线段两端点的距离相等的性质可得AB＝AE，根据等边对等角的性质可得∠B＝∠AEB，然后根据三角形的一个外角等于与它不相邻的两个内角的和列式求出∠C＝∠CAE，再根据等角对等边的性质求出AE＝CE，即可得出结论．

如图，在DC上取DE＝BD，连接AE．

∵AD⊥BC，∴AB＝AE，∴∠B＝∠AEB．在△ACE中，∠AEB＝∠C+∠CAE．

又∵∠B＝2∠C，∴2∠C＝∠C+∠CAE，∴∠C＝∠CAE，∴AE＝CE，∴CD＝CE+DE＝AB+BD．

∵AD=b，BD=a，∴AB==，∴DC=．

故答案为：．