题目内容
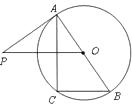
【题目】如图,已知 ![]() 是
是 ![]() 的直径,过点
的直径,过点 ![]() 作弦
作弦 ![]() 的平行线,交过点
的平行线,交过点 ![]() 的切线
的切线 ![]() 于点
于点 ![]() ,连结
,连结 ![]() .
.
(1)求证: ![]() ;
;
(2)若 ![]() ,
, ![]() ,求
,求 ![]() 的长.
的长.
【答案】
(1)证明:∵BC∥OP,
∴∠AOP=∠B,
∵AB是直径,
∴∠C=90°,
∵PA是⊙ O 的切线,切点为A ,
∴∠OAP=90°,
∴∠C=∠OAP,
∴△ABC∽△POA
(2)蛸:∵OB=2,
∴AB=4,OA=2,
∵△ABC∽△POA ,
∴ ![]() ,即
,即 ![]() ,
,
所以BC=8× ![]() =
= ![]() .
.
【解析】(1)根据已知BC∥OP,得出∠AOP=∠B,再根据AB是直径,PA是⊙ O 的切线,得出∠C=∠OAP,根据两组对应角相等的两三角形相似,即可证得结论。
(2)根据OB的长,就可求出AB的长,再根据△ABC∽△POA ,得出对应边成比例,即可求出BC的长。

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目