题目内容
【题目】如图所示,△ABC为等腰三角形,O是底边BC的中点,腰AB与⊙O相切于D点. 求证:AC是⊙O的切线.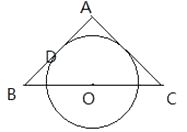
【答案】证明:过点O作OE⊥AC,垂足为E,连接OD,OA,
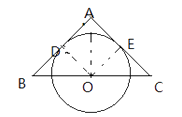
∵⊙O与AB相切于点D
∴OD⊥AB 又△ABC为
等腰三角形,O为底边BC的中点
∴AO是∠BAC的平分线
∴OE=OD,即OE是⊙O的半径
∴AC是⊙O的切线,得证.
【解析】证明一条直线是圆的切线的添加辅助线的方法:连半径,证垂直;作垂线,证半径。抓住关键的已知条件腰AB与⊙O相切于D点.因此连接OD,OA,要证AC是⊙O的切线.因此过点O作OE⊥AC,根据等腰三角形的三线合一的性质及切线的性质,得出AO是∠BAC的平分线及OD⊥AB,根据角平分线上的点到角两边的距离相等,得出OE=OD,即可得出结论。
【考点精析】关于本题考查的等边三角形的性质,需要了解等边三角形的三个角都相等并且每个角都是60°才能得出正确答案.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
【题目】下表记录的是今年长江某一周内的水位变化情况,这一周的上周末的水位已达到警戒水位![]() 米(正号表示水位比前一天上升,负号表示水位比前一天下降).
米(正号表示水位比前一天上升,负号表示水位比前一天下降).
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
水位 变化(米) | +0.2 |
| -0.4 |
| +0.3 |
|
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.








