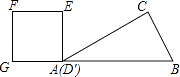题目内容
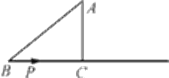
【题目】如图,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,动点P从点B出发沿射线BC以1cm/s的速度移动,设运动的时间为ts.
(1)求BC边的长;
(2)当△ABP为直角三角形时,求t的值.
【答案】答案见解析
【解析】试题分析: (1)直接根据勾股定理求出BC的长度;
(2)当△ABP为直角三角形时,分两种情况:①当∠APB为直角时,②当∠BAP为直角时,分别求出此时的t值即可;
试题解析:
解:(1)在Rt△ABC中,由勾股定理,得BC2=AB2-AC2=52-32=16.
∴BC=4 cm.
(2)由题意,知BP=t cm,
①当∠APB为直角时,如图1,点P与点C重合,BP=BC=4 cm,
∴t=4;

②当∠BAP为直角时,如图2,BP=t cm,CP=(t-4)cm,AC=3 cm,
在Rt△ACP中,AP2=AC2+CP2=32+(t-4)2.
在Rt△BAP中,AB2+AP2=BP2,
即52+[32+(t-4)2]=t2.
解得t=![]() .
.
∴当△ABP为直角三角形时,t=4或t=![]() .
.

【题目】为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
居民(户) | 1 | 2 | 3 | 4 |
月用电量(度/户) | 30 | 42 | 50 | 51 |
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A.中位数是50
B.众数是51
C.方差是42
D.极差是21
【题目】为了更好改善河流的水质,治污公司决定购买10台污水处理设备![]() 现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
现有A,B两种型号的设备,其中每台的价格,月处理污水量如下表:经调查:购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
A型 | B型 | |
价格 | a | b |
处理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
治污公司经预算购买污水处理设备的资金不超过105万元,你认为该公司有哪几种购买方案;
![]() 在
在![]() 的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.
的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为治污公司设计一种最省钱的购买方案.